線運動量がm・rVであるという完璧な答が隠れていた(2012年、日本)

剛体の表面を中心にした回転は並進運動に相当する(2012年、日本)(世界初!!)
線慣性を数学的に求めたとき、
なぜ積分区間0〜+2rで積分するのでしょう?
それは、
- 「剛体の表面を中心とする回転は並進運動に相当する」
からです。
均質でない剛体も含めて厳密に定義すれば、
剛体表面ではなく、<span style="color:red; font-size:12pt">重心から半径だけ離れた位置を中心にする回転</span>ですが、均質な場合が理解しやすいので、ここでは、一様な剛体で説明する。
一番分かりやすい例は、
紐に付けた重りをぐるぐると回転した後、手を放すことです。
ハンマー投げを思い浮かべるといい。
紐の長さをゼロにすれば、下図のような剛体棒の端(表面)を中心にした回転としてとらえることができる。
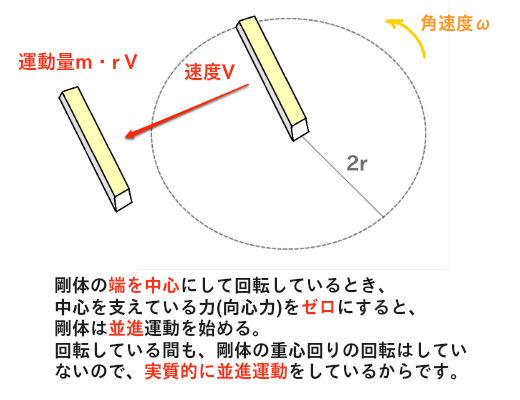
重心回りの回転と違って、このような回転では、回転中心を何らかの力(向心力)で固定しなければならない。向心力を人為的に加えているので、この向心力は重りの運動量には含まれない。
そして、手を放すと接線方向に直進し始める。
つまり、重りは回転している時でも実質的には並進運動をしている。
剛体棒は常に並進運動を続けているが、人為的な向心力によって、方向を無理やり変えさせられているに過ぎない。
転がりも全くこれと同じです。
転がりは接地点(剛体の端)回りの回転ですが、それは、
紐に付けた重りを回転させると同時に手を放すという行為を繰り返すことに相当する。だからこそ、転がりの線運動量もm・rVなのです。
重心回りの回転はいつまで経っても並進運動にはならない。
剛体の端を中心にした回転とそこが根本的に違う。
これが、剛体の線慣性および線運動量の真の姿です。
剛体の線慣性は単なる質量mではなく、
m・rであるという真実が原理的に言っても数学的にも完全に証明された。

「平行軸線定理」の最大の役割(2012年、日本)(世界初!!)
Biggest Role of Parallel-axis Theorem
平行軸線定理(平行軸の定理)は、
重心回りの角慣性(慣性モーメント)が決まれば、回転軸を平行移動したときの角慣性は、m・r2を加えればいいという定理です。rは質量中心から回転軸までの距離です。
一般的に、角慣性(慣性モーメント)の計算を簡便化する手段という認識しかない。
しかし、それは些細な一面に過ぎない。
実は、もっと重要な意味が隠れていた。
回転軸をどこに持って行っても良いのですが、
最も重要なのは、剛体の端(表面)を中心に回転するケースです。
それこそが、「平行軸線定理」の最大の役割と言っていい。
剛体の表面を中心にした回転は、前項で説明したように、
実質的な並進運動です。
そして、角運動量(全運動量)の変形によって、
\[ {\Large \fbox{ $ \displaystyle{ \begin{align} 平行軸線定理&は、線運動量がm\hspace{2pt}r\hspace{2pt}Vであることを示す。\\ 全運動量I_s\omega=&(I_c+m\hspace{2pt}r^{2})\omega\\ =&角運動量I_c\omega+線運動量\color{red}{m\hspace{2pt}r\hspace{2pt}V}\\ m:&質量\\ m\hspace{2pt}r:&線慣性\\ I_s=&I_c+mr^{2}:剛体表面回りの角慣性(平行軸線定理)\\ I_c:&重心回りの角慣性(慣性モーメント)\\ r:&質量中心から剛体表面までの距離\\ V=&r\hspace{2pt}\omega:瞬間的な並進速度\\ \end{align} } $ } } \]
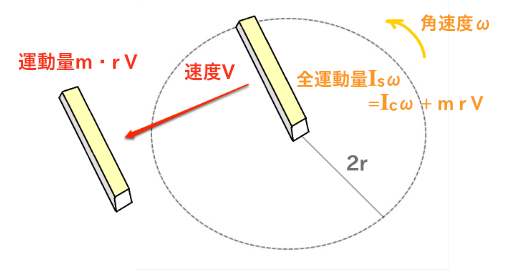
- 「平行軸線定理は線運動量がm・rVであることを示す」
積分計算を一々するまでもなく、
剛体の形状にかかわらず、必ずm・rVになる。
Icωは、剛体棒がその重心回りで回転しているときの角運動量と等価だが、本当にそういう回転をしている訳ではない。その角運動量に相当する向心力を加えていると言う意味です。
ここが少し理解しづらいが、純粋な回転運動成分を完全に分離すると、重心回りの角運動量になるということです。
それに対して、
重心〜表面の間の位置(重心と表面を除く)を中心にした回転は、
剛体自体も回転しているので、上記の式の意味が異なる。
やはり、人為的な向心力によって回転を維持している。
そして、人為的な向心力をゼロにしても、剛体自体の角運動量は残るので、
重心回りに回転しながら並進運動をすることになる。
つまり、剛体が持つ全運動量を完全に分離できない。
だからこそ、剛体表面を中心にした回転というのは特別なのです。
剛体の形状がいびつであれば、剛体の向きによって線運動量が異なる。
- 角慣性(角運動量)が回転軸の違いで異なるように、
- 線慣性(線運動量)も向きによって異なる。
それは自然なことです。
従来のように、線運動量がmV、つまり、形状や向きに依存しないと考えていたことはまさに、非科学です。
そして、何百年もの間、「平行軸線定理」の最も重要な意味を誰一人として理解していなかったということがよく分かる。
平行軸線定理(平行軸の定理)は、Huygens–Steiner定理とも呼ばれている。
Huygens(1629〜1695)とSteiner(1796〜1863) は同時代の人ではないので、100年以上もかかってやっと確定した定理のようです。
半径rは、並進方向と直角な方向であると言うことを明確に示している。
球体の運動量(転がりも含めて)は、半径rがどの方向も同じなので、
常にm・rVで表わされる。最も基本的で分かりやすい運動であると言える。
転がりの全運動量の変形から、この真理に気づいたのですが、
球体や転がりだけではなく、全ての剛体の運動に当てはまる原理です。
なぜなら、「平行軸線定理」という定理から導かれたからです。
- 「平行軸線定理が正しいと言うことは、
- 線運動量がm・rVであることもまた正しい。」
線運動量がm・rVであるという答えは、既に「平行軸線定理」の中にあった。
しかし、誰もそれに気づかなかった。気づこうともしなかった。
平行軸線定理を証明したSteiner氏でさえ気づかなかった。
そのことを天国で一番悔しがっているのはSteiner本人でしょう。
たまたま、私が最初にこの真実に気づいたにすぎない。
「平行軸線定理は、線運動量がm・rVであることを示す」という最も重要な解釈が加わることによって、平行軸線定理の存在価値が完全に確定した。
その意味で、平行軸線定理の別名は、
- 「Huygens–Steiner-蜂の子 定理(仮称)」
と呼ばれることになるでしょう。Huygens氏から実に300年以上もかかって、やっと完成したことになる。













