剛体の運動量は単なる重心の運動量ではないことが理解できた。
 
剛体各部の質点の線運動量はm_idxV_i(角運動量ではない)であり、
それを合計したもの、つまり、剛体全体の線運動量もやはりm・rVとなる。
剛体の密度が一様であってもなくても、m・rVである。
 
角慣性(慣性モーメント)と線慣性の計算方法は基本的には全く同じであり、
そのことから線慣性が単なる質量mではなく、m・rであることが明らかになる。
 
そして、それは、<span style="color:red; font-size:12pt">平行軸線定理(平行軸の定理)</span>の証明でもある。
 
 
 

角慣性を求める積分は質点に大きさがあることを暗に認めている(2012年、日本)

角慣性(慣性モーメント)を計算する積分計算は､
質点が大きさを持つことを前提にしている。


密度を使って式を立てていること自体が、
質点に大きさがあることを暗に認めていたと言うことです。


にもかかわらず､質点に大きさはないと主張してきた(参考文献[33])。
それは論理矛盾以外の何物でもない。
従来の考え方では、積分によって角慣性を求めることは数学的に言って不可能です。全てが矛盾している。


数学的に言って､長さのないものを合計(積分)すれば当然ゼロにしかならない。
微積分の「微」とはゼロと言う意味ではない。
この数学の基本をすっかり忘れている。
だからこそ、「質点の再定義」が必要なのです。


一番簡単な例、細い剛体棒(密度が一様)では以下のようになる。
教科書の典型的な計算例なので、この積分の意味を深く考える人はほとんどいないが、よくよく見れば、大きさのない質点を加算しているとは微塵も言えない。
大きさのない質点を加算していると考えるのは、まったく都合のいい解釈に過ぎない。


\[ {\Large \fbox{ $ \displaystyle{ \begin{align} 長さ2r&の\color{red}{剛体棒}の端を中心に回転している時の全運動量PL\\ PL=&I_s\omega=(I_c+mr^{2})\omega\\ =&\underbrace{I_c\omega}_{向心力の運動量}+\underbrace{\color{red}{m\hspace{1pt}r}\hspace{1pt}V}_{線運動量L}\\ I_s=& \int\limits_\color{red}{0}^{\color{red}{2r}}{\rho\hspace{2pt}{\rm d}x\hspace{2pt}x^{\color{red}{2}}}\\ =& \frac{m}{2r}\int\limits_0^{2r}{x^{\color{red}{2}}\hspace{1pt}{\rm d}x}\\ =&\frac{4}{3}mr^{2}\\ =&(I_c+mr^{2}):平行軸線定理\\ I_c=&\frac{m}{2r}\int\limits_{-r}^{r}{x^{\color{red}{2}}\hspace{1pt}{\rm d}x}=\frac{1}{3}mr^{2}\\ m:&質量\\ \rho=&\frac{m}{2r}:線密度\\ \rho\hspace{1pt}{\rm d}x:&微小部分の質量\\ \end{align} } $ } } \]

剛体の線運動量、線慣性の厳密な計算(2012年、日本)(世界初!!)

剛体の線運動量は<span style="color:red; font-size:12pt">剛体の形には依存しない</span>。
長さ2rの剛体棒のケースは一番簡単な例なので分かりやすい。


剛体棒の端を中心に回転しているとき、中心を維持している力、つまり向心力をゼロにした瞬間の運動量(線慣性)を計算する。


\[ {\Large \fbox{ $ \displaystyle{ \begin{align} 長さ2r&の\color{red}{剛体棒}が長さと直角な方向に進む時の線運動量L\\ L=&m_IV\\ =&\color{red}{m\hspace{1pt}r}\hspace{1pt}V\\ m_I=& \int\limits_\color{red}{0}^{\color{red}{2r}}{\rho\hspace{2pt}{\rm d}x\hspace{2pt}x}\\ =& \frac{m}{2r}\int\limits_0^{2r}{x\hspace{1pt}{\rm d}x}\\ =&\frac{m}{2r}\frac{4r^{2}}{2}\\ =&\color{red}{m\hspace{1pt}r}\\ m:&質量\\ m_I:&線慣性\\ \rho=&\frac{m}{2r}:線密度\\ \rho\hspace{1pt}{\rm d}x:&微小部分の質量\\ \end{align} } $ } } \]

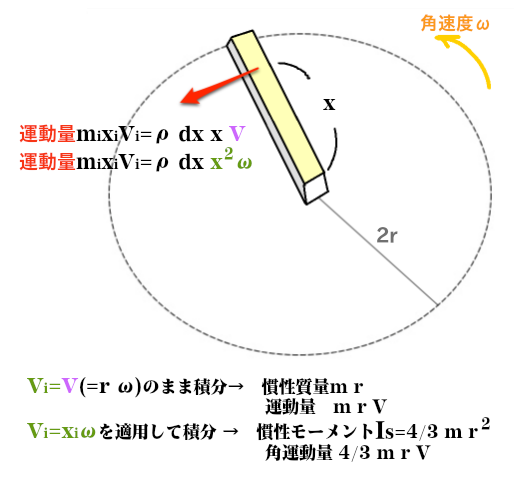
角慣性(慣性モーメント)を求める方法と基本的には変わりがない。
剛体内部の質点の線運動量はm_idxV_iなので、それを長さ方向に積分(厳密に言えば二重積分)すればいい。一回だけ積分したものが、m_ixV_iです。


回転の時に剛体各部の角速度ωが一定であるのと同様に､
並進のときは速度Vが一定(定数)なので、
m_ixV_iを積分することは、m_ix²あるいはm_ixを積分することになる。これがすなわち、角慣性(慣性モーメント)あるいは線慣性です。


角慣性と線慣性の積分計算の違いは、
V=r・ωと言う変形を加えるか加えないかの違いでしかない。
つまり、変数xが2次なのか1次なのかという違いです。


こんな単純な違いに300年以上誰も気づかなかったのが実に不思議です。
分かってしまえば当然ですが、これも「コロンブスの卵」ですね。


重みを掛けた値の和をモーメントと言う(参考文献[23]p.259)。

• r_i²という2次の重みが角慣性
• r_iという1次の重みが線慣性

ということになる。


重みが定数(0次)だとすると、それはモーメントではない。
従来、線運動量をmVと考えていたのは、モーメントではないと考えられていたからです。しかし、その考え方は、<span style="color:blue; font-size:12pt">平行軸線定理のmD²</span>に反する。


並進運動でさえモーメントであるという剛体の再定義がなされたことと、
線慣性に1次の重みがかかるということは同義です。


こう考えれば納得が行くでしょう。
剛体棒の端をつかんで回していた時に、その手を離した瞬間から、もっとも遠い端までにその作用が伝わるのに有限な時間がかかる。
だから、それはモーメントなのだと。
剛体が宇宙の広さと同じ大きさがあるという説明のことを思い出せば、理解できるはずです。


並進運動のときに1次の重みがかかっているからこそ、
回転運動の時には2次の重みになる。
そう考えれば、納得できるでしょう。


逆に、0次の重みから2次の重みに急に変化するのはあまりにも不自然です。回転と並進の間にそんな大きな差があるはずがない。
まさに論理の飛躍です。
線運動量がmVであるという従来の定義には何の根拠もない。

不均一な剛体の線運動量、線慣性の厳密な計算(2012年、日本)(世界初!!)

剛体の<span style="color:red; font-size:12pt">密度が一様でない</span>場合でも、平行軸線定理が成り立つ。
つまり、線慣性は必ずm・r(線運動量がm・rV)になることを意味する。


そのことを具体的に計算して確認しよう。


前項と同様に、長さ2rの剛体棒のケースで求めてみよう。


密度が一様でないため剛体棒の重心は偏っているが、その重心から半径rだけ離れた位置を中心に回転している場合を考えればいい。
それが平行軸線定理の意味に対応している。


やはり、中心を維持している力、つまり向心力をゼロにした瞬間の線運動量(線慣性)を計算する。


\[ {\Large \fbox{ $ \displaystyle{ \begin{align} 長さ2r&の\color{red}{均一でない剛体棒}が長さと直角な方向に進む時の線運動量L\\ 中心を&挟んで質量が\frac{2m}{5},\frac{3m}{5}。\\ 重心の&位置は中心から\frac{r}{10}だけ\frac{3m}{5}側に偏っている。\\ 重心位置&から半径rだけ離れた2つの位置A,Bを中心にしてそれぞれ回転させる。\\ どちらの&場合でも、線慣性はmrになる。\\ L=&m_IV\\ =&\color{red}{m\hspace{1pt}r}\hspace{1pt}V\\ m_I=&\frac{3m}{5r}\int\limits_\color{red}{\frac{r}{10}}^{r+\color{red}{\frac{r}{10}}}{x\hspace{1pt}{\rm d}x} +\frac{2m}{5r}\int\limits_{r+\color{red}{\color{red}{\frac{r}{10}}}}^{2r+\color{red}{\frac{r}{10}}}{x\hspace{1pt}{\rm d}x}: \frac{3m}{5}側の位置A\\ =&\frac{2m}{5r}\int\limits_{\color{red}{-\frac{r}{10}}}^{r\color{red}{-\frac{r}{10}}}{x\hspace{1pt}{\rm d}x} +\frac{3m}{5r}\int\limits_{r\color{red}{\color{red}{-\frac{r}{10}}}}^{2r\color{red}{-\frac{r}{10}}}{x\hspace{1pt}{\rm d}x}: \frac{2m}{5}側の位置B\\ =&\color{red}{m\hspace{1pt}r}\\ m:&質量\\ m_I:&線慣性\\ 線密度:&\frac{2m}{5r},\frac{3m}{5r}\\ \end{align} } $ } } \]


このように、偏った重心の位置から半径rだけ離れた2つの位置(位置A, B)を中心にして回転させた時、どちらの場合でも、
線慣性はm・rとなり、線運動量もm・rVとなる。


重心から半径rだけ離れた位置を中心に回転するとき、運動エネルギーと回転エネルギー、あるいは、線運動量と角運動量が完全に分離するからです。重心の位置と回転中心が一致している時には分かりやすいが、重心が偏っている場合でも、完全に分離している。それが、「平行軸線定理の最大の役割」です。


そして、上記の積分計算は、<span style="color:red; font-size:12pt">平行軸線定理のmD²</span>項の証明でもある。
平行軸線定理が剛体の密度が一様であってもなくても成り立つことはすでに確認したが、このような具体的な計算をしてみて初めて、そのことを納得できる。


こんな計算をするまでもなく、
1つの剛体(密度が一様であろうとなかろうと)が速度Vで直進している時、
それがどのような作用の結果であっても、線運動量が同じなのは当然です。


ただし、従来のようにそれがmVであると考えるのは間違いであり、
正しくは、線運動量はm・rVである。




惑星の角質量係数は惑星の構造・組成によって大きく異なる。
そのようなケースでも、線慣性は惑星の質量と大きさだけで決まる。
惑星の場合は、回転中心と重心は一致していると考えていいので、その点でも単純です。

角慣性が正しいのなら線慣性mrもまた正しい(2012年、日本)(世界初!!)

角慣性(慣性モーメント)を求めるための積分計算が正しいのであれば、
必然的に、線慣性を求めるための積分計算も正しい。
だから線慣性はm・rであり、それもまた正しい。


結局、これは、平行軸線定理を証明していることにもなる。
平行軸線定理の<span style="color:red; font-size:12pt">mD²</span>は、線慣性m・rに対応する。


平行軸線定理を用いれば、上記のような面倒な積分をする必要もない。




従来のように質量mを慣性質量と考え、運動量をmVと考えることは、
平行軸線定理(平行軸の定理)を否定することに等しい。


質点に大きさがなければ、質点に力を加えることもできない。
質点の表面を仮想の手でつかんで、質点の表面を中心にした回転ができない。
表面を中心にした回転ができれば、手を離することで並進運動を始めることができるけれども、大きさのない質点には不可能です。


結局、大きさのない質点は、自転もできないし、直進もできない。
運動することができない。
まったく、自然の摂理に反する。


従来の質点の科学とはそんな奇妙な世界の出来事であり、
科学的に言って何の意味もないものだと言うことです。


惑星の公転運動のときに、
惑星を大きさのない質点と見なすことは、まったくの空想の世界です。
惑星の軌道計算ができるのは、簡単に言えば、面積速度や向心力という側面から求めているだけで、大きさのない質点の存在を証明するものでは決してない。


角慣性(慣性モーメント)を積分計算する時だけ、都合よく、質点に大きさ(密度)を認めてしまう。


すべて、従来の考え方は、あまりにも都合のいい解釈と言わざるを得ない。


光は波であると同時に粒子であるという相反する考え方を受け入れてきた科学者たちにとって、惑星は剛体であると同時に質点であると考えることに何の疑問を持たないのでしょう。


力学の本の冒頭でそのことをすり込まれた(洗脳された)頭のいい学生がそのまま学者になるのですから、この洗脳を解くのは至難のわざかもしれない。頭が良ければ良すぎるほど、この洗脳は強固と言っていいでしょう。


しかし、どんなに正当性を主張しようとも、
剛体の線運動量が大きさのない質点と同じなどということは論理的に言って絶対にあり得ない。
そのことを、平行軸線定理が明白に示している。


大きさ(半径r)を持つ剛体の角慣性に半径rが含まれるのが当然なのと同様に、剛体の線慣性に半径rが含まれるのは当然のことです。


数多の科学者がこんな簡単なことを何百年も理解できなかったとは!!


こうして、「線慣性」も再定義される。

運動量の歴史がやっと始まる

転がりの場合でもm・rVになることは既に示した。
そして、物理数学的な厳密さにおいても、全く同じ結論が得られた。
剛体の形状には依存しないし、密度が一様であってもなくても同じである。

• 「剛体の線運動量はm・rV」
• 「剛体の線慣性はm・r」

という正しい定義が世界で初めて証明された。
科学的、論理的に導かれた当然の帰結です。


従来の「重力中心(重心)説」、つまり、剛体の並進運動を質点と等価とみなして、剛体の線運動量もmVと考えられていたことは、完全な誤りです。
その最たる例が、惑星の公転運動を質点と見なしてもいいと考えられていたことです。
質点とは大きさを持たないものと定義したこと自体がすべての矛盾の始まりだった。
そして、質量mが慣性質量あるいは重力質量と考えられていたこと自体も間違いだったことが証明された。


300年以上続いた負の歴史の終焉を迎えた。
歴史的な大転換点を迎えた。
運動量の歴史は、2012年にやっと始まった。
そう言っていいでしょう。