グリーンスピードを測定するためのツール
 グリーンの特性を示す2つの指標(グリーンスピード、傾斜の強さg)
グリーンの特性を示す2つの指標(グリーンスピード、傾斜の強さg) 斜面でのグリーンスピードを平面換算する計算式(1990, USA)
斜面でのグリーンスピードを平面換算する計算式(1990, USA) 傾斜の強さgを斜面でのグリーンスピードから求める計算式(1983, JAPAN)
傾斜の強さgを斜面でのグリーンスピードから求める計算式(1983, JAPAN)
![]() 真のグリーンスピード(2011,日本)
真のグリーンスピード(2011,日本)
- Jerry Lemons氏の論文(2008)が図らずも傾斜の強さgの正しさを証明している。
 トム・ワトソンは鋭い(1984年)
トム・ワトソンは鋭い(1984年)
もう一つ、Stimpmeterを応用して、段差のあるグリーンの狙い方について書かれたページ、PuttingZone(以前は図が描いてあって読みやすかったような気がする)も興味深い。

スティンプメーターの歴史は浅い
グリーンの速さ(グリーンスピード)を測るのが、スティンプメータです。
スティンプメータを使って転がった距離をグリーンスピード(green speed)と呼んでいる。
スティンプメータの歴史はそれほど古くはない。
スティンプメータの使用方法やスティンプメータの値も知っているようで知らない。
Webで検索してみると、海外サイトでは数多くヒットするのに、日本語サイトでは1、2箇所しかない。ゴルフ文化が日本には根付いていない1つの証拠ですね。

グリーンの特性を示す2つの指標(グリーンスピード、傾斜の強さg)
グリーンの特性を客観的、定量的に示すのはグリーンスピード(1つ目の指標)しかなかった。
傾斜は、角度という数値で示すことはできるが、それがどんな曲がり方をするかを具体的に示すものではない。そういう意味では、グリーンスピードと同列には扱えない。傾斜角は指標とは言えない。
グリーンスピードが8フィート程度が一般的で、ガラスのグリーンと言われるオーガスタが12フィートと言われれば、どのくらい速いのかが何となくイメージがつかめる。
でも、傾斜角が2度とか5%とか言われても、全くイメージがつかないので、何の役にも立たない。角度という数値を測るのは簡単ですが、そんなものを測っても全く無意味ということです。
2つ目の指標は、<span style="color:red; font-size:12pt">傾斜の強さg</span>です。
傾斜の強さとグリーンスピードという2つの指標を知ることが、グリーンの特性を正しく理解することになる。そのことは、2011年の今となっても、まだ普及していない。

斜面でのグリーンスピードの計算式(1990年 米国)
DOUGLAS BREDE氏による興味深いレポート(1990年11月/12月)を2004年頃に見たのはUSGA(アメリカゴルフ協会)
(http://www.usga.org/green/download/golf_course_managment/greens/measuring_green_speed.html)で、2011年現在はUSGA の「Green Section Record」にPDF化されている。
斜面で測定したグリーンスピードから平面での通常のグリーンスピードに換算するための補正式(2-4-0)を示している。
スティンプメーターは基本的には平らな面で測定するためのものなので、斜面でのグリーンスピード(平面換算した値)を直接計測する方法がなかったので、この補正式を考えたのだそうだ。
その実証実験として、人工的な斜面(0%〜5.6%の傾斜、0%のときに一般的なグリーンスピードと同等の8〜9フィート)で測定し、その補正式が正しいことを実証している。
さらに、実際のゴルフコースのグリーンでもテストして、6%(傾斜角3.4度)の傾斜まで、この式が成り立つことを確認したそうだ。
その補正式は、
\[ {\Large \fbox{ $ \displaystyle{ \begin{align} {\normalsize斜面でのグリーンスピード}&=\frac{2\times L_{u}\times L_{d}}{L_{u}+L_{d}}\ \ \ …{\normalsize(2-4-0)}\\ \end{align} } $ } } \]
Luが真っ直ぐの上りの進む距離で、Ldが下りの距離です。
LuとLdの差が6インチ以上ならこの式を使うように書かれている。
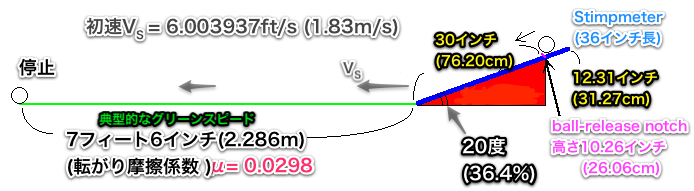
20度に傾けるというStimpmeterの使い方や単純な構造から言っても、あまり急な傾斜では有効な実験ができないのは明白でしょう。
それにしても、私より7年も遅れて、1990年になるまで、ゴルフ大国のアメリカでさえ、こんな簡単な式すら知らなかったというのが意外ですね。
誰もそれまでに考えたことがなかった、というのが実に不思議です。
そして、傾斜の強さを同様な計算で得られるということを、BREDE氏が言及できなかったというのもまた事実です。「傾斜の強さ」と言う概念自体が私が提唱するまでなかったので、仕方がない、というところですね。

傾斜の強さを求める計算式(1983年 日本)
私も上りと下りの比を使って、傾斜の強さgを求める式を1983年頃に考えたのですが、基本的な考え方は同じです。
式(1-4)を使うと、LuとLdは以下のように表される。
\[ {\Large \fbox{ $ \displaystyle{ \begin{align} L_{u}=&\frac{1}{f+g} \\ L_{d}=&\frac{1}{f-g} \ \ \ …{\normalsize(2-4-1)}\\ \end{align} } $ } } \]
f=1とし比をとって変形するか、単にfを消去すれば以下のようになる。
\[ {\Large \fbox{ $ \displaystyle{ \begin{align} {\normalsize傾斜の強さ}g=&\frac{L_{d}-L_{u}}{L_{d}+L_{u}} \ \ \ …{\normalsize(2-4)}\\ \end{align} } $ } } \]
これが、1983年に私が求めた式です。
逆に、式(2-4-1)からgを消去すれば、
\[ {\Large \fbox{ $ \displaystyle{ \begin{align} \frac{1}{f}=\frac{2\times L_{d}\times L_{u}}{L_{d}+L_{u}} \ \ \ …{\normalsize(2-4-2)}\\ \end{align} } $ } } \]
となり、式(2-4-0)と同じになる。1/fは、平面上で摩擦fだけが働いているときに転がる距離、つまり、グリーンスピードです。
この2つの式は、式(2-4-1)でfを消去するか、gを消去するかの違いでしかない。
斜面で上り/下りのグリーンスピードを測定すれば、平面換算のグリーンスピードも傾斜の強さも同時に求めることができる。一石二鳥の測定方法と言うわけです。
同じ初速で転がすので、摩擦fと傾斜の強さgという2つの値が連立方程式から求められるのは当然ですね。
例えば、Lu= 5フィート、Ld= 10フィートだとすれば(下りがちょうど2倍転がりやすい)、
-
グリーンスピード1/f 6.6フィート 傾斜の強さg 0.3333
ということがわかる。
g= 0.3333は傾斜として(曲がり方:
- このことから、斜面で速さを調べるというのは、かなり限定されることが分かる。BREDE氏が5.6%(3.2度)の傾斜までの実験しか出来なかったのは、そういう理由もあると思われる。
日本のグリーンでさえ5度(8.7%)程度まで存在する(参考文献[1])ことから考えても、5.6%というのはそれほど大した傾斜ではない。
ちなみに、BREDE氏によるレポートのグラフから計算してみると、はっきりした値が書いてないので概算ですが、傾斜の強さg= 0.06〜0.64と計算できる。
BREDE氏がどのようにして式(2-4-0)を求めたのかははっきりとは書かれてないが、同様の求め方をしたと思われる。ということは、逆の見方をすれば、私のこのサイトでの考え方が基本的には間違ってないということを間接的に証明しているという見方もできる。
結局、上りと下りの距離を測定すれば、グリーンの速さも傾斜の強さも同時にわかるということです。

USGAのグリーン
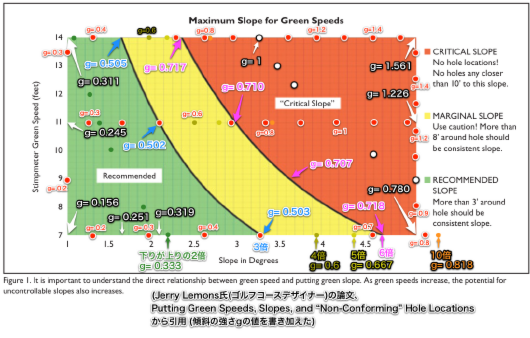
Jerry Lemons氏(ゴルフコースデザイナー)の論文、
Putting Green Speeds, Slopes, and “Non-Conforming” Hole Locations, USGA Green Section Record (Jul-Aug 2008), 21-25)は、<span style="color:red; font-size:12pt">傾斜の強さg</span>の妥当性を示していると言う点で、実に興味深い。
この論文の主旨は、最近のグリーンスピードの高速化を危惧して、カップをどこに切るべきかという問題に対して、ゴルフコースデザイナーという立場から、グリーンスピードと傾斜角を指標にして実用的に判断できるようにした、ということです。
この論文によれば、「USGA Course Rating 2007 System Guide」に、
「下りが上りの2倍が適度な傾斜」
「下りが上りの3倍はきつい傾斜」
と説明されている。これは傾斜の強さで言えば、式(2-4)で計算すると、それぞれ、
- g≈0.3
- g=0.5
に相当する。
つまり、傾斜の強さg=0.5でさえきつい、ということです。
傾斜角は、式(2-28)から、例えばトーナメントレベルのグリーンスピードGs=11ft、傾斜の強さg=0.5のとき、傾斜角θ≈2.04[deg]と計算できる。これは、Lemons氏の論文で言えば、Recommended SlopeとMarginal Slopeの境界に当たるので、実にもっともらしい。
ちなみに、教科書的な考え方で表した式(2-6-0)を使って式(2-28)を求め直して計算すると、傾斜角θ≈5.10[deg]と計算されるので、Lemons氏の実験結果からかけ離れている(<span style="color:blue; font-size:12pt">反例4</span>)。
下図はLemons氏の論文からの引用で、g値を書き加えたものです。
Critical Slopeとの境界がg≈0.71、Recommended Slopeの境界の傾斜の強さg≈0.5となっていて、実にきれいに当てはまっている。
これは、「下りが上りの3倍はきつい傾斜」がg=0.5ということとぴったりと符合する。
そして、式(2-4)から、g≈0.71は「下りが上りの約6倍」に相当する。
結局、下りが上りの3倍〜6倍(g=0.5〜0.71)の範囲がMarginal(境界)ということを示している。
この図が具体的にどのような実験によってプロットしたのかということは説明されていないが、下りが上りの何倍転がるのかということを調べたものと考えられます。実に全うなデータと言っていいでしょう。
この図の範囲で、傾斜の強さg=0.156〜1.561という値を示していることも興味深い。現実のグリーンでは、この程度の値であることを明確に示している。
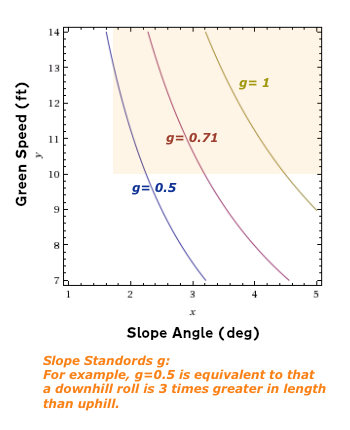
WolframAlphaを用いて 式(2-28)を 同じ範囲でプロットしたのが下図です。 Lemons氏の実測データと ほぼ一致しています。
以上のことから、<span style="color:red; font-size:12pt">式(2-28)</span>や<span style="color:red; font-size:12pt">式(2-4)</span>の正当性が実験的に証明された、ということです。Lemons氏に感謝したい。
実験で確かめられるのは、0< g< 1の範囲だけです。
傾斜の強さgが1以上になるとボールが止まらないので、上りと下りの比を調べることができないからです。g=1に限りなく近い0.999のようなケースでも、下りが1000倍も転がってしまうので、そんな場所を確保できない。実質的に計測不能です。
それに対して、式(2-28)は、どんな値であっても計算できる。
Lemons氏のように実験しなくても、計算だけでこのグラフを描くことができるし、このグラフの任意の点の傾斜の強さを計算で求めることも簡単にできる。
グリーンスピードと傾斜角の意味を正しく評価するには、式(2-28)が不可欠ということが言えます。

トム・ワトソンは鋭い(1984年)
トム・ワトソンが著書(参考文献[6])の中で、上りと下りのパットを交互に打って比較するという練習を勧めている。
経験的に、その重要性に気づいていたのでしょう。
上りと下りを比較するという考え方自体は、そう新しいものではないということです。
そして、アメリカでさえ、傾斜を科学的に扱うようになったのは、1980年台になってからで、つい最近ということです。
もう一つ、Stimpmeterを応用して、段差のあるグリーンの狙い方について書かれたページ、PuttingZone(以前は図が描いてあって読みやすかったような気がする)も興味深い。


 スティンプメーターの歴史は浅い
スティンプメーターの歴史は浅い USGAのグリーン
USGAのグリーン