摩擦の何倍かで表す

転がりの本質を知るために
最初のヒントは、傾斜をどう表すかだと言った。
それはどういうことだろうか。
学校で習ったことが頭から離れないと、最初どうしても傾斜角を考えてしまうものです。
しかし、傾斜角が同じだとしても、摩擦が弱ければ(ゴルフでは、速いグリーンという言い方をする)、傾斜が強くなったのと同じで大きく曲がることになる。
要するに、傾斜角を使っても、転がりの本質を求めることはできないということです。
それではどうしたらいいのでしょうか。
もっと単純に考えて、摩擦力と同じように、傾斜を力として考えればいいのです。それを傾斜の強さg(Slope Standards g)と呼ぶことにしよう。
摩擦の何倍の大きさなのかが傾斜の度合いを表している。
垂直抗力について疑問を感じる人がいるかもしれないが、それは実質的に無視できる(→垂直抗力)。
今後の計算式の中では、
平面での摩擦力(芝の抵抗)をf、傾斜の強さをgで表す。
ともに正の値として、方向は符号で表す。
摩擦f=1として傾斜の強さg値による変化を見る
具体的な数値計算では、f=1として計算して(垂直抗力を参照)、g値による変化を調べる。
そうすれば、平面を基準にして傾斜の転がり方を知ることでできる。
g= 0.5とかg= 1の場合にどのような転がり方をするのかを考えるということです。
このようにすれば、摩擦gと傾斜fを引いたり加算したりすることで簡単に計算できる。
逆に傾斜角という絶対値を入れてしまうと、本質が見えなくなってしまう。
但し、関係が分かるように、原則的には、fを式の中に入れます。
例えば、上りと下り
傾斜による力は、常に下り方向(後述の+Y方向)に働く。
摩擦のY成分は、進む方向によって符号が変化する。
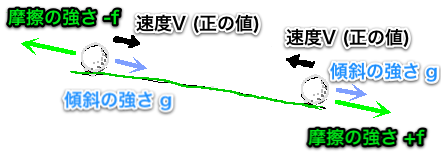
例えば、真っ直ぐの上りでは、f+gという力がかかって減速が速まり、
真っ直ぐの下りでは、-f+gという力がかかって抵抗が弱くなったり、加速することもある。
傾斜の強さgの具体的な値・計算式
(1)傾斜の強さg=1のときの傾斜角
(2)典型的な段差の傾斜の強さg
(3)斜面のグリーンスピードと傾斜の強さgを求める計算式
(4)グリーンスピード・傾斜角(計測値)と傾斜の強さgとの関係

