ボールの中心回りのモーメントN_c (2003年 日本)

傾斜角θの傾斜の上のボールには、傾斜によって発生するボールの中心回りのモーメントN_cと転がり摩擦によるモーメントN_fという2つのモーメントが働いている。

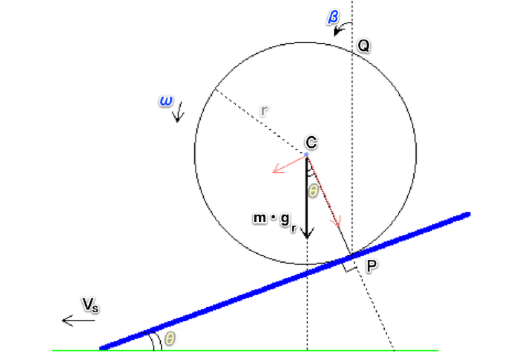
接地点Pを支点として(仮想的にPは固定したまま)、PQという軸が角加速度dβ/dtで倒れると考える。
点Pの回りの慣性モーメント I_p は、球の慣性モーメント I_c (=2/5 m･ r² ) にm･ r² を加えたものです。


\[ {\Large \fbox{ $ \displaystyle{ \begin{align} I_{p}=& I_{c}+m\cdot r^{\hspace{3pt}2}\\ =&\frac{7}{5}m\cdot r^{\hspace{3pt}2}…{\normalsize(2-19-0)} \end{align} } $ } } \]


点Ｐの回りのモーメント N_p (摩擦は除く)は
\[ \fbox{ $ \displaystyle{ \begin{align} N_{p}=m\cdot g_{r}\cdot \sin{\theta}\cdot r\\ \end{align} } $ } \]
接点Pの回りのモーメントと角加速度βの間には、 I_p ･dβ/dt = N_p という関係があるので、
\[ \fbox{ $ \displaystyle{ \begin{align} \frac{{\rm d}\beta}{{\rm d}t}=\frac{{\rm d}\omega}{{\rm d}t}=\frac{N_{p}}{I_{p}}\\ \end{align} } $ } \]
PQという軸が角加速度dβ/dtで倒れることで、ボールの回転dω/dtに転換 され、 結局、この角加速度は同じ値です。( dβ/dtとdω/dtの関係 )


よって、ボールの中心回りのモーメントNc(摩擦を除く)は、
\[ {\Large \fbox{ $ \displaystyle{ \begin{align} N_{c}=&I_{c}\frac{{\rm d}\omega}{{\rm d}t}=\frac{I_{c}}{I_{p}}N_{p}\\ =&\frac{2}{7}N_{p}\\ =&\frac{2}{7}m\cdot g_{r}\cdot\sin{\theta}\cdot{r}…{\normalsize(2-20-0)} \end{align} } $ } } \]


これは、 「倒れ ることの連続が転がり」という概念( 参考資料[16] )を数式化したもの ととらえることができる。


ただし、このような面倒なことを考えなくても､「 並進エネルギーと回転エネルギーの比は5:2 」 に示したように､ 斜面方向に働く力m g_r sinθ の2/7倍の力が回転運動に使われるので､直ちに式(2-20-0)が得られる 。

---

転がり摩擦によるモーメントN_f

これは単純に、以下の式で表される。
\[ {\Large \fbox{ $ \displaystyle{ \begin{align} N_{f}=\mu\cdot m\cdot g_{r}\cdot\cos{\theta}\cdot{r}…{\normalsize(2-21)}\\ \end{align} } $ } } \]

---

転がりの傾斜角(傾斜の強さg=1)

傾斜の強さg=1というのは、摩擦と傾斜の強さが一致する場合なので、言い換えれば、2つのモーメント、N_cとN_fが一致するということです。


\[ {\Large \fbox{ $ \displaystyle{ \begin{align} N_{c} &=N_{f}\\ \therefore\theta &=\arctan{(\frac{7}{2}\mu)}…{\normalsize(2-24)}\\ \end{align} } $ } } \]
例えば、典型的なグリーンスピードG_S= 7.5ft(2.286m)のグリーンの場合、転がり摩擦係数μ≈ 0.0299なので、
\[ {\Large \fbox{ $ \displaystyle{ \begin{align} \theta\approx5.97[deg]\\ \end{align} } $ } } \]


これは、実にもっともらしい。
実際のグリーンの傾斜はせいぜい5度程度、典型的なものは3度程度と言われているからです。


グリーンの転がり摩擦係数で示したように、間違った方法で求めた摩擦係数μ≈ 0.075の場合で計算してみると、θ≈ 14.7[deg]という値なってしまうが、これはどう見ても大きすぎる。この点から考えても、μ≈ 0.075という値が間違いとわかる(<span style="color:blue; font-size:12pt">反例2</span>)。


g=1からは転がりの真の意味を知ることができる。
そのことを1983年から28年間も気づかなかった。
転がりの最大静止摩擦の性質や撃力を加えた直後のメカニズムの本当の意味を理解することができる。

---

傾斜の強さgとグリーンスピード・傾斜角の関係(2003年、日本)

本サイトでは、傾斜の強さgを傾斜の強さの何倍かという相対的な値として考えている。


傾斜の強さg、正確に言えば、摩擦fとの比g/fなので、これを絶対値で表すと、N_c/N_fです。
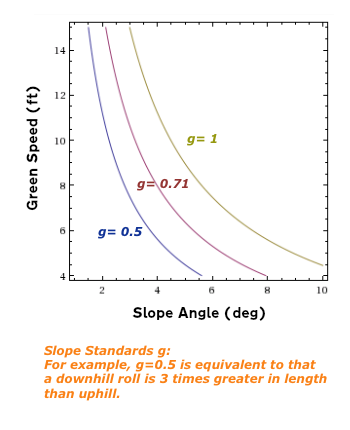
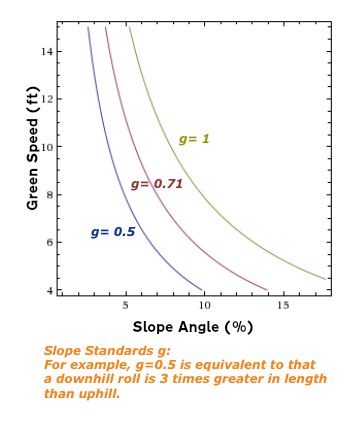
この式で明確になるのは、傾斜の強さgはパーセント勾配と比例するということです。
\[ {\Large \fbox{ $ \displaystyle{ \begin{align} g=\frac{N_{c}}{N_{f}}=&\frac{2}{7}\frac{\tan{\theta}}{\mu}\\ =&\frac{10}{7}\frac{g_{r}\cdot\tan{\theta}\cdot G_{s}}{V_{s}^{\hspace{3pt}2}}\\ =&\frac{10}{7}\frac{g_{r}\cdot \frac{P}{100}\cdot G_{s}}{V_{s}^{\hspace{3pt}2}}…{\normalsize(2-28)}\\ &{\normalsize P:パーセント勾配指定} \end{align} } $ } } \]

上図は、g=0.5, 0.71, 1の3つのケースで､WolframAlphaの等高線プロットコマンドを使って、描画したものです。クリックすると実行します。
以下のwidgetは、Wolfram|Alpha Widgetsを利用して､任意のg値の等高線グラフを描く。


例えば、典型的なグリーンスピードG_S= 7.5ft(2.286m)のグリーン(μ≈ 0.0299)の典型的な段差(傾斜角26.57[deg]≈50%)では、
\[ {\Large \fbox{ $ \displaystyle{ \begin{align} g\approx4.8 \\ \end{align} } $ } } \]

これも、実にもっともらしい。


間違った方法で求めた摩擦係数μ≈ 0.075の場合で計算してみると、g≈1.9という値になる。
典型的な段差の傾斜角は、通常のグリーンの傾斜角(3度〜5度程度)の約5〜9倍なのに、g≈1.9という値は傾斜の強さgとしては小さ過ぎる。通常のグリーンの傾斜の強さgは0.5前後なので、g≈4.8という値のほうが妥当です。
この点から見ても、典型的なグリーンスピードG_S= 7.5ft(2.286m)の転がり摩擦係数μ≈ 0.075という値が全くの見当違いであることが証明された(<span style="color:blue; font-size:12pt">反例3</span>)。


Jerry Lemons氏の論文(2008)はこの式(2-28)が正しいことを証明している。


Lemons氏のように実験で測定してこのグラフを描けるのはせいぜいg=0.7程度までで､g≧1(ボールが止まらないケース)では唯一この式(2-28)だけです。


つまり、段差を正確に評価できるのは、式(2-28)だけということです。
例えば､典型的なグリーンスピードG_S= 7.5ft(2.286m)のグリーンの典型的な段差(傾斜角26.57[deg])は(つまり、g≈4.8)、上記のwidgetを用いれば､オーガスタのG_S=12ftでは18[deg](33%)くらいに相当すると簡単に分かる。


今まで､そして現在でも、ゴルフコースデザイナーは、段差を正確に評価する手段を知らずに、グリーンをデザインしているということです。
今後は､上記のwidgetを使用して科学的にグリーンをデザインできるようになるでしょう。


Augusta fast(G_S=12〜15ft)の場合、

• 傾斜角が3度(5.2%)のグリーンならg= 0.8～1
• 傾斜角が5度(8.8%)のグリーンならg= 1.4～1.7

という値になる。ガラスのグリーンと言われる転がり方、曲がり方を見れば、もっともらしい値と考えられる。


実際にカップを切れるのは、図1で示したようにg=0.5〜0.71の範囲(黄色)が限度で、斜度で言えば、G_S=12ftのときは1.9〜2.7度(3.3〜4.7%)、15ftのときは1.5〜2.1度(2.6〜3.7%)までです。