支点Pの回りの角加速度とボールの中心Cの回りの角加速度は等しい

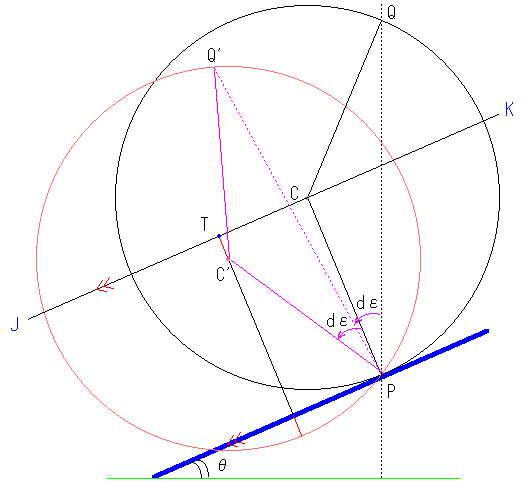
Pを支点として(Pを固定して)軸PQが微小時間の間に 角度dε だけ倒れ込むと考えてみる。そのとき、図のように、仮想的にはボールが斜面に 距 離 $\overline{TC\hspace{1pt}'}$ だけ 沈み込んだ ような状態になる。上図は、分かりやすくするために、dεを誇張して描いている。
角度 $\angle CPC\hspace{1pt}'$ もdεに等しい。
だから、沈み込まずに普通に転がったとすれば、支点Pの先のボールの表面が $\overline{TC\hspace{1pt}'}$ と同じだけ斜面に近づけばいい。つまり、角度dεだけ回転することになる。


あるいは、 軸PCがPC'に倒れ込む と考えても同様です。


倒れ込む角度と回転する角度は等しい ということです。
と言うことは、角速度や角加速度についても同様のことが言える。
つまり、支点Pの回りの角加速度dβ/dtは、ボールの中心Cの回りの角加速度dω/dtと等しい。
\[ \fbox{ $ \displaystyle{ \begin{align} \frac{{\rm d}\beta}{{\rm d}t}=\frac{{\rm d}\omega}{{\rm d}t}\\ \end{align} } $ } \]
注意してほしいのは、 支点Pの回りの「慣性モーメント」は、中心Cの回りの値とは異なる という点 です。だからこそ、角加速度が同じであっても、「力のモーメント」は異なる値になる。