回転エネルギー・並進エネルギーと転がり摩擦の本当の意味

転がり摩擦による減速
平面でボールが減速する時に、
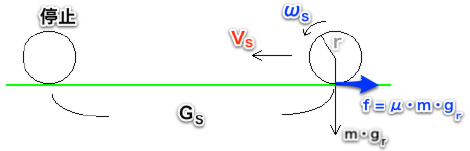
ボールには転がり摩擦μ・m・ gr しか加わっていない。
この時、ボールが持っている回転エネルギーと並進エネルギーがどのように失われるだろう?
そして、転がり摩擦係数μはどんな式として表されるでしょう?
この本当の意味を理解するのに、ボールの中心を引っ張って加速することの意味を考えてみるといい。
並進エネルギーと回転エネルギーの比は5:2
見方を変えて、重心をFGという力で引っ張ってみよう。
平面ではそういうことはあり得ないが、斜面では現実にそういう力が加わっている。
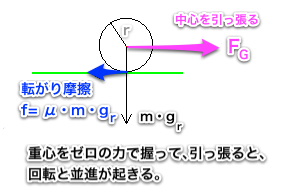
ゼロの力で重心を握っていると仮定する。
このことによって、ボールは並進と同時に回転を起こす。
ゼロの力で重心を握りつつ、引っ張って、滑らずに転がったとすれば、重心に作用した力FGの一部が回転エネルギーに変換され、残りが並進の運動エネルギーに変換される。すなわち、FGのすべてが並進の運動エネルギーに変換されるのではないということです。そのエネルギー比は、
\[ {\Large \fbox{ $ \displaystyle{ \begin{align} \frac{1}{2}m\cdot V_{s}^{\hspace{3pt}2}:\frac{1}{2}I\cdot \omega_{s}^{\hspace{3pt}2}=5:2 \end{align} } $ } } \]
ただし、球の慣性モーメント
言い換えれば、重心に作用した力FGの2/7倍が回転に使われ、5/7倍が並進運動に使われる。
教科書では、斜面(傾斜角θ)の運動方程式から並進の加速度aを
\[ {\Large \fbox{ $ \displaystyle{ \begin{align} a=\frac{5}{7} g\cdot \sin{\theta} \end{align} } $ } } \]
と求めている。
でも、この係数5/7の意味を説明しているものを見たことがない。
結局、力の比5:2なので、並進に使われる力は5/7倍ということを意味している。
この意味を理解していることが、以下のように転がり摩擦を考える時に、非常に重要なのです。
転がり摩擦の5/2倍の力が並進エネルギーを失わせる
だから、転がり摩擦によって減速する場合には、これと逆に考えればいい。
転がり摩擦fがボールと面との接点に働くということは、その摩擦fより大きな力(摩擦fの7/2倍の力)が重心に作用していることに等しい。重心に作用する力のさらに5/7倍の力(トータルで言えば摩擦fの5/2倍の力)が、並進の運動エネルギーを失わせることになる。
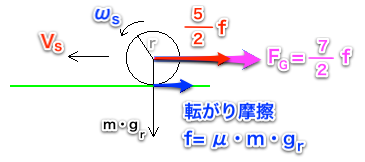
転がり摩擦は「接地点回りの回転」に作用する(2012年、日本)(世界初!!)
本質的に言えば、
その結果として、並進エネルギーと回転エネルギーを同時に失う。
決して、直接、並進と(中心回りの)回転に作用しているのではない。
転がり摩擦係数μの正しい求め方
だから、転がり摩擦係数μを並進運動から求めても、回転運動の式から求めても一致する。
つまり、式で表すと、
\[ {\Large \fbox{ $ \displaystyle{ \begin{align} &\frac{1}{2}m\cdot V_{s}^{\hspace{3pt}2}=\frac{5}{2}\mu\cdot{m}\cdot{g_{r}}\cdot G_{s} \\ &\frac{1}{2}I\cdot \omega_{s}^{\hspace{3pt}2}=N\cdot\alpha=\mu\cdot{m}\cdot{g_{r}}\cdot G_{s} \end{align} } $ } } \]
Nは転がり摩擦によるモーメントμ・m・gr・rで、
重力加速度gr=9.8m/s2、
αはボールが回転した角度でGs/rに等しい。
球の慣性モーメント
\[ {\Large \fbox{ $ \displaystyle{ \begin{align} \mu=\frac{1}{5}\frac{V_{s}^{\hspace{3pt}2}}{g_{r}\cdot G_{s}} \end{align} } $ } } \]
が得られる。一致するのが当然です。
滑らずに転がっているので、v=r・ωという関係で拘束されているからです。
一致することから、単純に、係数が5/2であると答えてもいい。
これで、教科書的な考え方で表した式(2-6-0)が間違いということがはっきり理解できた。
そして、転がり摩擦係数を求める時は、回転と並進のどちらで考えてもいいけど、回転運動から求めるのが単純で間違いがない。

転がり摩擦係数μの具体的な値を比較してみる
転がり摩擦係数μの具体的な値を比較してみれば、さらに確信できる。
教科書的な考え方で典型的なグリーンスピードGS= 7.5ft(2.286m)から求めた間違った値μ= 0.075は、school-for-championsにあるデータ、鉄路の上の鉄の車輪の転がり摩擦係数0.001や乾いた舗装道路の上の車のタイヤの転がり摩擦係数0.015に比べて、大きすぎる。
タイヤに比べて5倍というのはちょっと考えにくい。
それに比べて、式(2-8)で求めた値μ=0.0299は、タイヤの約2倍の大きさで、この程度なら、あり得る。
タイヤをStimpmeterから転がして、舗装した道路に転がしたと想像してみてください。7.5ft(2.29m)の5倍、37.5ft(11.43m)も転がるでしょうか?
約2倍の15ft(4.57m)くらいなら、あり得そうですね。
これだけを見ても、教科書的な考え方から求めた値μ=0.075が非現実的だとすぐに分かる(<span style="color:blue; font-size:12pt">反例1</span>)。
ガラスのグリーンと言われるオーガスタのグリーンでも、典型的なグリーンスピードの2倍程度にすぎないが、それでも相当な速さに感じる。
タイヤがいくら転がりやすいと言っても、5倍も転がりやすいというのはあり得ない話です。
オーガスタのグリーンの上のボールと舗装道路の上のタイヤがほぼ同じ速さということになる。そう言われれば、そんな程度のような感じがするでしょう。
単純に考えて、硬質で滑りやすいゴルフボールを柔らくて抵抗のある芝の上で転がす場合と、滑りにくいゴムのタイヤを固いアスファルトの上で転がす場合は、接するお互いの性質がちょうど入れ替わっているようなもので、結果として、転がりやすさが近いのは実にもっともらしい。
まとめ
転がり摩擦で減速するということは、
回転エネルギーを失うと同時に、並進エネルギーも失う。
直方体が滑るときは滑り摩擦の力を重心の位置まで単純に平行移動することができるけれども、転がり摩擦の場合にはそう簡単には行かない。
そのことに十分注意しなければいけない。



