教科書的な考え方の落とし穴

教科書的な考え方をすると正しい値は得られない
芝とボールの間の転がり摩擦係数μを知っても、斜面での曲がり方を考える時にまったく意味はないのですが、教科書的な考え方をすると間違いを犯してしまう、という面白い事実に気づくので、少し考えてみましょう。
高校の物理の教科書にも転がり摩擦係数の具体的な値がいくつか載っていますが、ほとんど説明がなくてピンとこないので、グリーンの転がり摩擦係数というはっきりした事例を知っておくのは意味がある。
Stimpmeter値(グリーンスピードGS)から計算します。
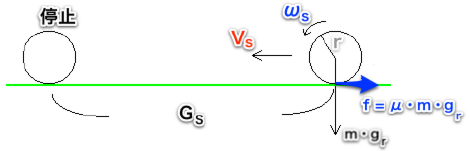
従来の考え方は、並進の運動エネルギーが、
\[ {\Large \fbox{ $ \displaystyle{ \begin{align} \color{blue}{\frac{1}{2}mV_{s}^{\hspace{3pt}2}=\mu\cdot{m}\cdot{g_{r}}\cdot G_{s}…{\normalsize(2-6-0)}}\\ \end{align} } $ } } \]
のように表されると考えて、転がり摩擦係数μを求める。
\[ {\Large \fbox{ $ \displaystyle{ \begin{align} \color{blue}{\mu=\frac{1}{2}\frac{V_{s}^{\hspace{3pt}2}}{g_{r}\cdot G_{s}}…{\normalsize(2-8-0)}} \end{align} } $ } } \]
gr は重力の加速度(9.8m/ s2 )、 Vs は初速(Stimpmeterから飛び出た時の速度)です。
例えば、Stimpmeter( Vs = 1.83m/s)で測定した 典型的なグリーンスピード GS = 7.5ft(2.286m)の場合、 μ= 0.075 と計算される。
ProbableGolf では 参考文献[15] (p.438)から引用した この式を用いた値が示されている 。
一見もっともらしいので信じてしまいますが、実は、この 式(2-6-0)は間違い です。
ProbableGolf のKen Tannar氏に間違いを指摘したところ、 回転エネルギーとの合計が摩擦によって失われる というもっともらしい考え方を言ってきた。
基本的な間違いは理解してくれたが、 ProbableGolf の記述 は 8年経っても修正されていない (2003.5.26〜2011.09.18現在)。
この 教科書的な考え方 から求めた式は、 4つの反例によって完全に否定されます 。
- (反例1)ボールの中心を引っ張る
- (反例2)傾斜の強さg=1のときの傾斜角
- (反例3)典型的な段差の傾斜角
- (反例4)Lemons氏の論文

正しい考え方
仕事N・αによって最初の回転エネルギーが失われるで、
\[ {\Large \fbox{ $ \displaystyle{ \begin{align} \frac{1}{2}I\cdot \omega_{s}^{\hspace{3pt}2}=&N\cdot\alpha \\ =&\mu\cdot{m}\cdot{g_{r}}\cdot G_{s}…{\normalsize(2-7)} \end{align} } $ } } \]
αはボールが回転した角度でGS/rに等しい。
Nは転がり摩擦によるモーメントμ・m・gr・rで、これによって減速する。
そして、球の慣性モーメント
\[ {\Large \fbox{ $ \displaystyle{ \begin{align} \mu=\frac{1}{5}\frac{V_{s}^{\hspace{3pt}2}}{g_{r}\cdot G_{s}}…{\normalsize(2-8)} \end{align} } $ } } \]
例えば、典型的なグリーンスピードGS= 7.5ft(2.286m)の場合、
μ= 0.02989715571になる。
これが正しい理由は、「ボールの中心を引っ張る」にまとめてあります。
そして、この転がり摩擦係数は、実は、<span style="color:red; font-size:12pt">同時に、静止摩擦係数でもある</span>。

転がり摩擦の法則性は実は未解明(2011年まで)
意外だけれども、教科書にも、ネット上でも、なぜか、転がり摩擦係数を求める式を簡単に見つけることができない。
検索して見つけた中で唯一信憑性のある説明が、長岡技術科学大学機械系 太田研究室(太田浩之 准教授)の以下の資料です。
- トライボロジー講義資料(2011年用)(参考文献[16])
トライボロジー(tribology)という言葉は一般人には馴染みがなく、私も今回(2011年)初めて知ったのですが、摩擦・摩耗・潤滑に関する学問のことだそうです。どちらかと言うとボールベアリングとか工学的な感じですね。
この講義資料の「第4章 転がり摩擦(Ver.2)」の転がり摩擦の歴史(P.76)に以下のように説明されている。
- 「転がり摩擦の研究は行われてきたが,
- その法則性はまだ確立されていない」
これでやっとうなずけました。
はっきりした正解がないので、誰も式をあえて書こうとしない、ということなんですね。
参考文献[15]では18個の資料を参照していながら、間違った式を示しているということは、転がり摩擦係数を正しく求める式が書かれた文献はないという1つの証拠と言っていい。
そんな基本的なことを誰でも知っているはずだと思うけれども、誰も正しく理解していない。
高校の物理の授業でも、滑り摩擦係数を求める式は詳しく説明するのに、なぜか、転がり摩擦係数を求めることに関しては、曖昧な説明で終わらせてしまっている。
にもかかわらず、鉄道の車輪とかゴムタイヤの転がり摩擦係数の値だけが示されていて、具体的な測定データが何か、どうやって求めたのかを高校の先生も教えてくれなくて、疑問だけが残ってしまったことを記憶している。
転がり摩擦・転がり摩擦係数という言い方以外に、「転がり抵抗・転がり抵抗係数」という言い方もある。
摩擦も抵抗する力という意味では、摩擦抵抗という言い方もするので、大した違いはない。
結局、どんな力が働いていたとしても、その力が球体にトルクを働かせるということに変わりはない。
難しい学問的な転がり摩擦の発生メカニズムは学者の研究に任せるとして、基本的には、一定の抵抗がトルクとして働く、という考え方から求める必要がある、ということに疑問の余地はない。
決して、転がり摩擦力を重心まで平行移動して、まるで滑り摩擦の問題のように解くことはできない。
転がり摩擦の法則性、転がりの原理はほぼ明らかになった(2011年、日本)
転がりの摩擦は1種類(曲面抵抗)ということがはっきり解明できた。
学者が行うような学問的な厳密な理論とは言えないけれども、
1つ1つ論理的に考えて行けば、この当然の帰結に至る。



