「真の転がり」になるまでの時間、すなわち、
パットしてから「前のめり転がり」が続く時間を正確に計算する方法は、意外にも、誰も知らない。
それは、「転がりの基本原理」を実は今まで正しく理解していなかったためです。
 
正確に計算する方法は、どのように回転が生じるのか(転がりの基本原理)を考えてみればわかる。
 

「真の転がり」になるまでの時間は意外に短い(概算)

 
 
計測データ(その1)のケースで、
最初の1.667ftの経過時間tは､平均速度から概算すると、
\[ {\Large \fbox{ $ \displaystyle{ \begin{align} \frac{V_{0}+V_{0}\sqrt[]{\frac{5}{7}}}{2}t=&1.667ft\\ \therefore t\approx0.1975[s]\\ &t:時間\\ &V_{0}:初速(9.15ft/s)\\ \end{align} } $ } } \]
と計算できる。思っている以上に短時間で「真の転がり」に移行することが分かる。
 
「真の転がり」になった時の速度は、「真の転がり」の長さで示した通りなのでいたって簡単に求めることができる。こんな簡単なことでさえ、今まで誰も答えられなかったのが、本当に不思議です。
 

「真の転がり」になるまでの時間(正確な計算)(世界初!!)

 
 
正確に言えば､「はずみ車モデル」を用いるべきだが､
結果的にはこの時間に関しては同じ結論に達する。
 

 
 
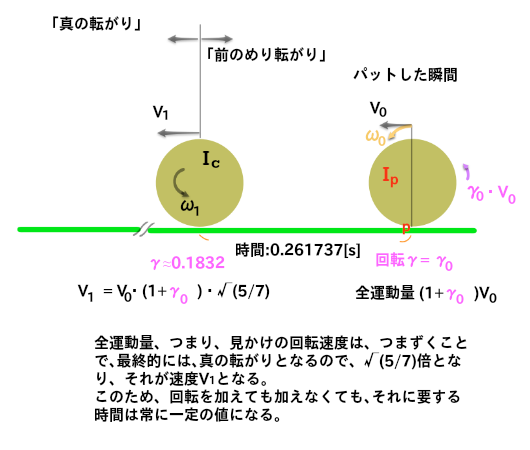
並進速度V₀で打ち出しつつ、回転γ₀・V₀を加えた場合、
微小時間ごとの接地点回りの角運動量は、

• I_pω₀dt = I_p(V₀+γ₀・V₀)/r dt

から始まって、

• I_pω₁dt = I_p(V₀+γ₀・V₀)√(5/7)/r dt

まで変化して行く。
 
一方、ボールの中心回りの角運動量は、最初はゼロなので、増加量は「真の転がり」になった瞬間の角運動量そのもの、

• I_cω_t = I_c(V₀+γ₀・V₀)√(5/7)/r

です。
 
そして、微小時間ごとの角運動量は直線的に減って行くと考えられるので、単純に、以下のように平均値として求められる。
\[ {\Large \fbox{ $ \displaystyle{ \begin{align} 初速&V_{0}に回転\gamma_{0}V_{0}を加えて打ち出されたとき\\ I_{p}&\omega_{0}{\rm d}t+…+I_{p}\omega_{1}{\rm d}t\\ = I_{p}&\frac{\omega_{0}+\omega_{1}}{2}t= I_{p}\omega_{0}\frac{1+\sqrt[]{\frac{5}{7}}}{2}t\\ =I_{c}&\omega_{1}=I_{c}\omega_{0}\sqrt[]{\frac{5}{7}}\\ \therefore t=&\frac{4}{7}\frac{\sqrt[]{\frac{5}{7}}}{1+\sqrt[]{\frac{5}{7}}}\approx0.261737[s]\\ つまり&、回転を加えても加えなくても常に一定の時間。\\ すなわち&、前のめり転がりの長さは初速V_{0}に比例する。\\ &I_{p}=\frac{7}{5}mr^{2}:接地点回りの慣性モーメント\\ &I_{c}=\frac{2}{5}mr^{2}:ボールの中心回りの慣性モーメント\\ &V_{0}:並進の初速\\ &\omega_{0}=\frac{V_{0}+\gamma_{0}V_{0}}{r}\\ &\omega_{1}=\omega_{0}\sqrt[]{\frac{5}{7}}\\ &t:前のめり転がりの時間[s]\\ &\gamma_{0}:加えた回転を並進速度換算する係数\\ &　　\gamma_{0}\geq0:正回転\\ &　　\gamma_{0}\leq0:バックスピン\\ \end{align} } $ } } \]
接地点回りの慣性モーメントI_pについては、ここを参照。
 
概算した値0.198[s]に近いので、レベル的に適切な計算と言っていい｡
 
初速が速くても遅くても､回転を加えても加えなくても､時間は常に同じ、という意外な結果が得られた。
グリーンスピードにも依存しない。
 
にわかには信じがたいかもしれませんが､
最初の全運動量(速度)の√(5/7)倍の並進速度になるという一定の関係があるので、初速(加えた回転も含めて)が大きくなればなるほど､倒れやすくなるため､√(5/7)倍の並進速度(真の転がり)になる時間は一定になる。
 
でも、考えてみればもっともらしい。
時間が一定と言うことは、言い換えれば、
真の転がりになるまでの距離(前のめり転がりの距離)は、初速に比例するということです。
 
最初から「真の転がり」であれば、転がる距離は初速の2乗に比例する。
エネルギーをすべて失う時は初速の2乗に比例し、
エネルギーの形を変える時は初速に比例する、
というのは、実にもっともらしい。
 
パットの初速と言うのは、どんなロングパットでも桁違いな大きさということはないので、真の転がりになるまでの距離は、それほど大きな違いはないということを示唆している｡
 
前のめり転がりが短い時間・短い距離である理由がこれで明らかになった。
 
これは、現実とも一致する。
 
教科書に書かれた滑らなくなった時の速度は完全に間違っているので､言うまでもなく､教科書に書かれた滑らなくなるまでの時間も､当然間違っている。
 
もっともらしい嘘と言うのは､信じやすいものですが、
今後は､もうだまされることはないでしょう。

「前のめり転がり」の長さ

 
 
正確に言えば､「はずみ車モデル」を用いるべきだが､
以下のような単純な平均で求めたものもそれほど大きな違いはない。
単純なモデルとしての近似計算値を知ることも意味はある。
 
\[ {\Large \fbox{ $ \displaystyle{ \begin{align} &前のめり転がりの長さ[ft]\\ =&\frac{1}{0.3048}\frac{V_{0}+V_{1}}{2}t\\ =&\frac{1}{0.3048}V_{0}\frac{1+(1+\gamma_{0}) \sqrt[]{\frac{5}{7}}}{2}t\\ =&\left\{{\frac{V_{0}}{0.3048}\sqrt[]{\frac{5}{7}}}\right\}\frac{2}{7}\frac{1+(1+\gamma_{0}) \sqrt[]{\frac{5}{7}}}{1+\sqrt[]{\frac{5}{7}}}\\ &ただし、t=\frac{4}{7}\frac{\sqrt[]{\frac{5}{7}}}{(1+\sqrt[]{\frac{5}{7}})}\approx0.261737[s]\\ &V_{0}:並進の初速[m/s]\\ &V_{1}=V_{+0}\sqrt[]{\frac{5}{7}}:前のめり転がりの終端速度、つまり、真の転がりの初速\\ &V_{+0}=(V_{0}+\gamma_{0}V_{0})=V_{0}(1+\gamma_{0}):全運動量､すなわち速度\\ &t:「前のめり転がり」の時間[s]\\ &\gamma_{0}:加えた回転を並進速度換算する係数\\ &　　\gamma_{0}\geq0: 正回転\\ &　　\gamma_{0}\leq0: バックスピン\\ &　　\gamma_{0}=-1:「真の転がり」はゼロだが､「前のめり転がり」はある。\\ &　　\gamma_{0}=\gamma_{T}=\left\{{\sqrt[]{\frac{7}{5}}}\right\}-1\approx+0.1832:「真の転がり」に相当する回転\\ &　　真の転がりに相当する正回転を加えても、\\ &　　すぐには真の転がりにはならない。\\ \end{align} } $ } } \]
 
上記のように距離が求められるが､
並進速度V₀と終端速度V₁の平均速度になっている部分に疑問も持つかもしれない。特に､なぜ、V₀なのか?
 
それは､γ₀= −1というバックスピンを考えることで理解できる。
パッティングでγ₀= −1のような強烈なバックスピンは打てないので､そんなことを考える必要はないように思えるかもしれない。
 
でも、γ₀= −1というバックスピンを考えてみることで理解できることがある。

γ₀= −1のとき

 
 
γ₀=−1の意味で説明したように､前のめり転がりの長さを計算する時の初速はあくまでも､V₀であって、V₀+γ₀・V₀ではない。
 
この点は極めて重要です。
 
仮に､V₀+γ₀・V₀が初速であるとして方程式を求めてみると､
γ₀= −1のときに、前のめり転がりの距離もゼロになってしまう。
つまり､前進も後退もしないことになってしまう。
これは一見すると､正しいように思えるけれども､正しくない。
 
γ₀= −1のときに、並進速度は、V₀からゼロへと変化する。
それが一瞬の間に起きると考えること自体間違っていることはよく考えてみれば理解できるはずです。
 
時間を求める時には､V₀+γ₀・V₀を使用したのに､
どうして､距離を求める時にはそうならないのか､
疑問に思うのは十分理解できる。
私自身､一時はそう考えていたからです。
 
それでは､計測される並進初速とは､加えた回転も含めたものだろうか?
そうではないのは疑いようがない。
 
回転があるからその分だけ並進速度が大きくなるということはあり得ない。
 
真の転がりのときに､角速度の分だけ並進速度が増える訳ではないことを考えてみればよく分かる｡
 
時間を求める時には､運動量の変化を計算しているので､最初に全運動量が来るのは正しい。
 
並進速度は､つまずくことで倒れるための回転速度のように振る舞うけれども､加えた回転は､並進速度のように振る舞うような原理はどこにもないからです。
 
結局､矛盾は無い。
 
逆に言えば､
γ₀= −1というバックスピンのときに、前進も後退もしないと考えることの方が都合がよすぎて、よほど､疑わしい。