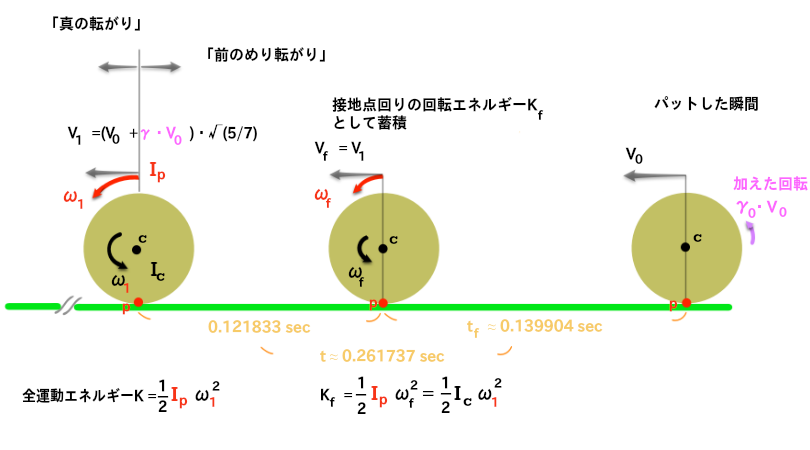
「前のめり転がり」でエネルギーを失わない

「前のめり転がり」は、つまずき続けることで､エネルギーを失わずに､
並進速度V₀・√(5/7)の真の転がりになる。
それは、計測データの解析から明らかです。


パットしてからボールが止まるまでの全体の距離を合理的に説明するには､エネルギーを失わないと考える以外にない。


従来の滑り摩擦モデル(Skid Model)ではこの現実を説明できない。

計測データでは並進速度の方が早く減速する

その一方で､計測データ(その3)を見ると､
並進速度は角速度の約倍のペースで減速するという現実も示している。


ここだけを見ると､エネルギーを失っているように見える。
この点では、従来の滑り摩擦モデルのほうが正しいように見える。


滑り摩擦モデルが信じられてきたのは､この点だけで判断したためです。

それぞれの矛盾

上記の2つの事実は矛盾しているように見える。


滑り摩擦モデルと「前のめり転がり」のどちらが正しいのでしょう?


滑り摩擦モデルでは、エネルギーを失うので､失ったエネルギーが復活することはあり得ない。滑り摩擦モデルが破綻しているのは疑いようがない。


それでは､「前のめり転がり」のモデルはどうだろう?


「前のめり転がり」のモデルが正しいと仮定すると､
エネルギーを失ったように見えて､実は失っていない、
ということを示唆している。


それを合理的に説明するのがフライホイールモデルです。

フライホイール(はずみ車)とは

フライホイール(flywheel、はずみ車)とは、Wikiにあるのように、


「回転系の慣性モーメントを増やすことで回転速度の変化を緩やかにする。
あるいはフライホイールを回転させることで運動エネルギーを蓄え、
別の機械要素にトルクを与えるエネルギー源として利用する構成もある。」




要するに､
慣性モーメントの大きなものが回転エネルギーとして蓄えて､
それをゆっくりと解放して行くということです。

前のめり転がりの「フライホイールモデル」

転がりの基本原理から前のめり転がりの間に、接地点回りで回転が起きる。
接地点回りの慣性モーメントI_pは中心回りの慣性モーメントI_cより大きい。


これがフライホイールの役割をする。


そして､接地点回りの回転エネルギーとして蓄積する。
蓄積した後で､ボール中心回りの回転へと転換する。


このようにして、全体のエネルギーを失うことなく､真の転がりになる。


フライホイールは､一般的には、エネルギーを蓄える部分とそれを利用する部分は別のものです。


ところが、前のめり転がりでは､ボールという1つの物体で構成される点で､非常に特殊でユニークなフライホイールと言えます。


これがフライホイール効果であることはなかなか気づかない。
私も､この点に気づくのに半月以上かかってしまった。

接地点回りでエネルギーを蓄積する

前のめり転がりではエネルギーを失うことなく真の転がりになることから、
並進速度はV₀→V₀・√(5/7)に変化するが、
並進速度と角速度は同じペースでは変化しない。


前のめり転がりの前半では､
フライホイール効果によって、接地点回りの回転エネルギーとして蓄積される。
並進速度がV₀→V₀・√(5/7)に変化することによって失うエネルギーがいったんフライホイールに蓄積される。


並進速度がV₀・√(5/7)まで減速した時の角速度ω_fは、

• ω_f ≈ 0.45*V₀/r

このω_fは接地点回りの角速度であるが､同時に中心回りの角速度でもある。
エネルギー的には､中心回りの角速度ω₁ = √(5/7)*V₀/rまで増加するだけのエネルギーを接地点回りの回転エネルギーとして保持していることを意味する。


これがフライホイール効果です。


計測データ(その3)のグラフを見れば､まさしく､ほぼこの通りの値が計測されている。


角速度がω_fになったときに持っている回転エネルギーは､接地点回りの瞬間的な回転エネルギーの積算です。
接地点回りの瞬間的な回転が連続することで角速度ω_fに達した時に持っている回転エネルギーと、単に､中心回りで角速度ω_fで回転している場合の回転エネルギーは明らかに異なる。


並進速度と角速度の傾き(加速度､角加速度)だけを見れば､
滑り摩擦モデルとフライホイールモデルが一致しているように見える。

フライホイールに蓄積したエネルギーを解放する

こうやって、「前のめり転がり」の前半で、
角速度は約半分だけ増加する。




そして、前のめり転がりの後半では､
この蓄積されたエネルギーが解放され､それまでと同じペース(角加速度が一定)で角速度がω₁まで上昇するとともに､
並進速度はV₁のまま等速で進む。


蓄積されたエネルギーは､角運動量を増加させるという形で転換される。
中心回りの回転エネルギーが増加するように見えるけれども､見えない形で蓄積していたエネルギーが見える形に変わっただけなので､全体のエネルギーは変化しない。


そして､真の転がりになる。


このようにして､
前のめり転がりの間にエネルギーを失うことなく､真の転がりになる。

瞬間的な計測データだけ見てもフライホイール効果を知ることはできない

一般的なフライホイール(はずみ車)を考えてみれば納得が行く。
加えたエネルギーをゆっくりとした回転として保持している。大きな慣性モーメントだから､角速度は小さくても､見た目より大きなエネルギーを保持できる。


外見上の並進速度と角速度だけでどれだけのエネルギーを持っているかは判断(計算)できない。


つまり、ストロボ撮影の手法で「前のめり転がり」のときの並進速度や回転角度を計測したとしても、エネルギーがどれだけ蓄積されているかを瞬間瞬間のデータだけで知ることはできない。


真の転がりが始まるときの速度､つまり､転がる全体の距離を評価して初めて､正しい判断ができる。

非現実的な「滑り摩擦モデル」
そして、現実に矛盾しない「フライホイールモデル」

前のめり転がりの前半部分では､外見的には､エネルギーを大きく失っているように見えるため、従来は､転がり摩擦の10倍程度の滑り摩擦が働いていると考えたくなったのは無理もない。


転がり摩擦の10倍もの滑り摩擦が、真の転がりになった途端、10分の1の転がり摩擦に切り替わると考えることがいかに不自然かを考えてみるだけで､滑り摩擦モデルが非現実的であることは明らかです。


氷の上で本当に滑っているならいざ知らず､
芝の上のボールには滑り摩擦などという架空の力は最初から存在しない。


一方､フライホイールモデルでは、
「前のめり転がり」の前半で蓄積したエネルギーを後半で解放するため、前のめり転がりから真の転がりにスムースに移行することを無理なく説明できる。現実に矛盾しない。

慣性の法則の拡張

「前のめり転がり」の後半では､角速度は一定の角加速度で増加する。
これは、一種の慣性の法則です。


一般的に､慣性の法則とは等速直線運動(エネルギーが保存される)と考えられている。


前のめり転がりでもエネルギーが保存されるという慣性の法則の基本部分は一致しているが、エネルギーの形が変わるので､加速度が発生する。


つまり、慣性の法則の本質は､エネルギーの保存という点です。


フライホイールに回転エネルギーを蓄積する時には､並進速度は一定の加速度で低下しつつ、角速度も一定の角加速度で増加する。


そして、フライホイールに保存された回転エネルギーが解放する時には､それまでの角加速度を保ったまま進む。


角加速度が一定するのも慣性のためです。


つまり、慣性の法則の本質はエネルギーの保存で､
エネルギーの形が変わらなければ､速度は一定(等速直線運動)となり、
エネルギーの形が変化する時には､加速度・角加速度が一定(等加速度・等角加速度運動)になる、ということです。


このように､慣性の法則は拡張される。

角運動量は理解しているようで理解していない

転がりの角運動量とは何か?
それすら、ちゃんと理解していなかった。

前のめり転がりの時間

「前のめり転がり」の前半の経過時間､つまり、
接地点回りの回転エネルギーに転換する時間t_fは以下で示すように､

• t_f= 0.139904 sec

並進速度がV₀・√(5/7)まで落ちて､観測上はエネルギーを失ったように見えるまで､時間t_fが経過する。


そして、「前のめり転がり」の後半では、
慣性の法則の拡張によって､角加速度を保ったまま､蓄積されたエネルギーを中心回りの回転に転換して行き､エネルギーを失うことなく､真の転がりに達する。


つまり､時間は角速度に比例するので､前のめり転がりの全体の時間tは､

• t = 0.261737 sec

このようにして、「前のめり転がり」の時間は､常に一定となる。


\[ {\Large \fbox{ $ \displaystyle{ \begin{align} 初速V_{0}に回転&\gamma_{0}V_{0}を加えて打ち出されたとき\\ 並進速度が&V_{0+}からV_{1}に落ちることでそのエネルギー差が全て\\ 接地点回り&の回転エネルギーとして蓄積される時間t_{f}は､\\ I_{p}&\frac{V_{0+}}{r}{\rm d}t+…+I_{p}\frac{V_{1}}{r}{\rm d}t\\ = I_{p}&\frac{\frac{V_{0+}}{r}+\frac{V_{1}}{r}}{2}t_{f}= I_{p}\frac{V_{0+}}{r}\frac{1+\sqrt[]{\frac{5}{7}}}{2}t_{f}\\ =I_{c}&\omega_{f}=I_{c}\frac{V_{0+}}{r}\sqrt[]{\frac{2}{7}\frac{5}{7}}\\ \therefore t_{f}=&\frac{4}{7}\frac{\sqrt[]{\frac{2}{7}\frac{5}{7}}}{1+\sqrt[]{\frac{5}{7}}}\approx0.139904[s]\\ 慣性の法則&の拡張によって､同じ角加速度を保ったまま進むので､\\ t=&t_{f}\frac{\omega_{1}}{\omega_{f}}\\ =&\frac{4}{7}\frac{\sqrt[]{\frac{5}{7}}}{1+\sqrt[]{\frac{5}{7}}}\approx0.261737[s]\\ つまり&、回転を加えても加えなくても常に一定の時間。\\ &I_{p}=\frac{7}{5}mr^{2}:接地点回りの慣性モーメント\\ &I_{c}=\frac{2}{5}mr^{2}:ボールの中心回りの慣性モーメント\\ &V_{0}:並進の初速\\ &V_{0+}=V_{0}+\gamma_{0}V_{0}: 加えた回転を含めた実質的な初速\\ &V_{1}=V_{0+}\sqrt[]{\frac{5}{7}}\\ &\omega_{f}=\sqrt[]{\frac{2}{7}\frac{5}{7}}\frac{V_{0+}}{r}\\ &\omega_{1}=\sqrt[]{\frac{5}{7}}\frac{V_{0+}}{r}\\ &t:前のめり転がりの時間[s]\\ &t_{f}:接地点回りの回転エネルギーとして蓄積する時間[s]\\ &\gamma_{0}:加えた回転を並進速度換算する係数\\ &　　\gamma_{0}\geq0:正回転\\ &　　\gamma_{0}\leq0:バックスピン\\ \end{align} } $ } } \]

なぜ「滑り摩擦モデル」が信じられてきたのか?

以上のフライホイールモデルを理解した上で計測データ(その3)を見れば､なぜ滑り摩擦モデルが信じられてきたのかという理由(真相)がはっきり分かる。


と同時に､フライホイールモデルの正しさが証明される。


結局､並進速度と角速度の計測値が、滑り摩擦が作用しているかのように見えたことが、「滑り摩擦モデル」を信じてしまった本当の理由です。


接地点回りでエネルギーを蓄積するので､外見上の並進速度と角速度だけでは判断できないのに、表面的な値だけで判断してしまったため、誤った理論(滑り摩擦モデル)が何百年も信じられ続けてきた。


たしかに滑っているように見える上､ 通常は転がり摩擦が働き､ここでは滑り摩擦が働くと考えるのがシンプルで、全てを摩擦と言うもので説明できるはずだと考えてしまった。世界はシンプルな原理が作っているものだ､と考えたくなったのも無理はない。

前のめり転がりの長さ

フライホイールモデルでの「前のめり転がり」の長さを求める式は､以下のようになる。


計測データ(その3)で､真の転がりになるまでの長さが23inchesと表示されているが､これは計測値ではなく明らかに計算値です。
しかし､どのような計算式を使ったのかは不明です。


そこで、以下の式を用いて計算してみよう。
回転を加えていないと仮定すると､
0.573603 m(22.5828 inches= 前半12.5617in +後半10.0211in )と計算できる。


これは､計測値(23inches)に極めて近いが､この計測システムがフライホイールモデルを使用しているはずはないので､滑り摩擦モデルで計算した上で､何らかの補正をしていると思われる。


\[ {\Large \fbox{ $ \displaystyle{ \begin{align} フライ&ホイールモデルに基づいた前のめり転がりの長さ:\\ 前半の長さ=&\frac{V_{0}+V_{1}}{2}t_{f}\\ =&\frac{V_{0}+(V_{0}+\gamma_{0}V_{0})\sqrt[]{\frac{5}{7}}}{2}\frac{4}{7}\frac{\sqrt[]{\frac{2}{7}\frac{5}{7}}}{1+\sqrt[]{\frac{5}{7}}}\\ =&\frac{V_{0}\left\{{1+(1+\gamma_{0})\sqrt[]{\frac{5}{7}}}\right\}}{2}\frac{4}{7}\frac{\sqrt[]{\frac{2}{7}\frac{5}{7}}}{1+\sqrt[]{\frac{5}{7}}}\\ 後半の長さ=&V_{1}*(t-t_{f})\\ =&(V_{0}+\gamma_{0}V_{0})\sqrt[]{\frac{5}{7}}\cdot\frac{4}{7}\frac{\sqrt[]{\frac{5}{7}}-\sqrt[]{\frac{2}{7}\frac{5}{7}}}{1+\sqrt[]{\frac{5}{7}}}\\ =&V_{0}(1+\gamma_{0})\sqrt[]{\frac{5}{7}}\cdot\frac{4}{7}\frac{\sqrt[]{\frac{5}{7}}\left\{{1-\sqrt[]{\frac{2}{7}}}\right\}}{1+\sqrt[]{\frac{5}{7}}}\\ 第1項は&直進距離を求めるので､\\ 加えた回転&を含めた実質的な初速V_{0+}ではなく、純粋な初速V_{0}である。\\ \therefore t_{f}=&\frac{4}{7}\frac{\sqrt[]{\frac{2}{7}\frac{5}{7}}}{1+\sqrt[]{\frac{5}{7}}}\approx0.139904[s]\\ t=&\frac{4}{7}\frac{\sqrt[]{\frac{5}{7}}}{1+\sqrt[]{\frac{5}{7}}}\approx0.261737[s]\\ &V_{0}:並進の初速。\\ &V_{0+}=V_{0}+\gamma_{0}V_{0}: 加えた回転を含めた実質的な初速\\ &V_{1}=V_{0+}\sqrt[]{\frac{5}{7}}\\ &t:前のめり転がりの時間[s]\\ &t_{f}:接地点回りの回転エネルギーとして蓄積する時間[s]\\ &\gamma_{0}:加えた回転を並進速度換算する係数\\ &　　\gamma_{0}\geq0:正回転\\ &　　\gamma_{0}\leq0:バックスピン\\ \end{align} } $ } } \]

「フライホイールモデル」と「滑り摩擦モデル」の決定的な違い

前のめり転がりの長さは､あまり重要ではない。


どちらのモデルで計算しても､計測データ(その3)の例で10cm程度の差しかないからです。グリーンの不均一さが原因なのか測定誤差なのか判断が難しい。


前のめり転がりの長さだけでは､どっちのモデルが正しいかは判断できない。


最も重要なことは、真の転がりが始まる時の速度､つまり、ボールが停止するまでの距離です。


2つの計測データの解析でも明らかなように､「滑り摩擦モデル」では、<span style="color:blue; font-size:12pt">全体の距離の誤差が26%</span>というひどい値になってしまう。


「滑り摩擦モデル」では「真の転がり」の長さを正しく計算できない。


ここが、「滑り摩擦モデル」が完全に破綻していることを示す疑いようもない事実です。


そして、計測しなければ滑り摩擦係数がどんな値かも分からないため､事前に転がる距離を計算できないことも、「滑り摩擦モデル」が役に立たない点です。


しかも､計測して滑り摩擦係数という都合のいい架空の値が分かったとしても､
肝心の真の転がりの長さがまともに計算できないのでは､何の役にも立たない。


「滑り摩擦モデル」を使ってリアルなシミュレーションをすることは不可能です。


フライホイールモデル(前のめり転がり)では、事前に計算できる。
より現実に近いシミュレーションができる。
滑り摩擦係数などという架空の値を使う必要がないからです。