普通のケース(必ず止まる)の転がり方でさえ予想外だった。
それでは、ｇ≧１の転がり方はどうだろう?

放物曲線に近いのは唯一g=1のときだけ

摩擦と傾斜の強さが等しい(f＝g= 1)ときに、初めて止まらなくなる。そして、放物運動のようにすぐに真っ逆さまになることが計算でわかる。放物運動に関する我々の知識から言えば、ごく当然と感じる。


この時に横方向の越える距離がたぶん最大(0.333)で、傾斜がもっときつくなれば、すぐに曲がってその距離が短くなると予測したくなる。


でも、実際に計算してみると、そうならない。
簡単な実験をしてみれば、確認できる。

---

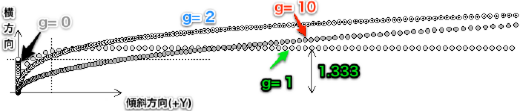
傾斜が強くなればなるほど放物運動と真逆の曲線を描く

下図に示すように(これもアンケートと同様の条件）、傾斜が強くなればなるほど、横方向に関して言えば、弱い傾斜を必ず越える。
g=1の10倍の傾斜でも、最初は急激に曲がるのに、真っ逆さまにならない。

現実のグリーンでも、止まらないことは確かにある。
でも、止まらなくなる最初のg=1の10倍の傾斜なんて普通はない。


グリーンの傾斜角はせいぜい５度程度なので、10倍の傾斜とは 単純計算すれば傾斜角50度 となるが、そんなグリーンは現実にはあり得ない。


グリーンキーパーは 芝を短くカット することで曲がりやすくしているが、普段の10倍以上も転がりやすくするなんてこともない。 前に説明した ように、グリーンの速さを10倍速くすることは傾斜の強さgを10倍にするのと同じです。


グリーンの摩擦係数から 厳密に計算 してみても、 せいぜいg= 1程度、典型的な段差でさえg= 4 くらいです。


要するに、普通はあり得ないような強い傾斜(例えばg= 10)であっても、 我々が想像しているような曲がり方にはならない ということです。


言い換えれば、止まらないでグリーンからこぼれてしまうような斜面では、 ボールが曲がって行く方向は傾斜の方向とは一致しない ということです。最初から真っ直ぐ下っているような場合を除いて。