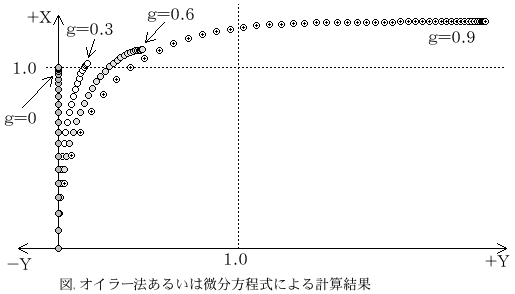
オイラー法で転がりの数値計算 (同じ強さでいろいろな方向に打つ)

2011.09.30
JavaScriptで数値計算(1)
式(3-2)を元にしたわずか数十行のプログラムで数値計算できる。
ブラウザーのJavaScriptを有効にすると実行できます。
g≧1を指定した時は、転がり続けるので、適当な位置で計算を止めています。
<span style="color:red; font-size:12pt">別の数値計算の例</span>もある。
アンケートと同様に、打ち出す方向θ0= 0の例をいくつか計算すると、以下のようになる。
初速V0= 1です。
| 傾斜の強さg | 停止位置 | 時間T | |
| X座標 (横方向) | Y座標 (傾斜方向) | ||
| 0 | 1 | 0 | 1 |
| 0.3 | 1.0230 | 0.1649 | 1.0989 |
| 0.6 | 1.0989 |
0.4688 | 1.5626 |
| 0.9 | 1.2539 | 2.3687 | 5.2634 |
距離1を1メートルと考えた場合でさえ、X方向(横方向)に 2~25センチも余計に転がる ことがわかる。g=0.9という強い傾斜では、25%以上も越える。
カップの直径が10.79cm(半径5cmちょっと) なので、 2~25センチという値は 無視できない 。
g=0.3という比較的弱い傾斜でさえ、3mのパットなら、7cm近くオーバーしてしまうので、 ギリギリで入らない ということを意味する。
g= 0.6のように結構大きく曲がる場合には、1メートルの短いパットであっても、オーバーしたくなくて、 カップにちょうど入るように打ちたくなる が、そうしようとすればするほど、約10センチもオーバーしてしまうので、どうしてそんなにオーバーしたのか混乱するばかりで、そういう経験から、結局、 強めに打って曲がる前に入れようという考え方しかできなくなっていた わけです。
カップの横からのパットが難しいと思い込んでいたのは当然で、 このメカニズムを知らないでいくら狙っても、まぐれでしか入らない 。