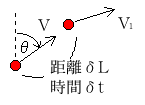
微小時間δｔの間に､速度VからV₁に変化し､微小距離δL進んだとする｡微小時間なので、速度Vのまま方向θも変化しないで、真直ぐ転がると考える。初速V₀,初角度θ_０､最初の時間はゼロとする。原点(0,0)から転がり始めるものとする。(座標の取り方）
 

---

傾斜方向の速度の変化

 
 
速度のY成分が、V_yからV_1yに変化したとする。
\[ {\Large \fbox{ $ \displaystyle{ \begin{align} V_{y}\hspace{5pt}=& a\cdot V_{0} \\ V_{1y}=& b\cdot V_{0}\\ \end{align} } $ } } \]

---

力のY成分

 
 
傾斜による力(傾斜の強さ)も含めて、ボールに加わる力のY成分は、
\[ {\Large \fbox{ $ \displaystyle{ \begin{align} {\normalsize力のY\hspace{3pt}成分:}&(f\cdot\sin{θ}-g)\cdot F\\ &{\normalsize(ただし、F\hspace{3pt}は正の値)} \ \ \ …{\normalsize(3-1)}\\ \end{align} } $ } } \]

---

微小時間の間に傾斜方向に進む距離

 
 
Y方向に進む微小距離δLyは、式(1-4)より、
\[ {\Large \fbox{ $ \displaystyle{ \begin{align} \delta L_{y}=&\frac{{V_{0}}^{2}}{F}\frac{(b^{\hspace{2pt}2}-a^{\hspace{2pt}2})}{-(f\cdot\sin{\theta}-g)} \\ =& \frac{b^{\hspace{2pt}2}-a^{\hspace{2pt}2}}{-(f\cdot\sin{\theta}-g)} \\ \end{align} } $ } } \]
となる。基準は平面(初速V₀= 1,F= -1)なので、-V₀²/F= L= 1と見なす。
 
δL_yの正負をよく見ると、g≦１の場合はY方向に関して加速している部分があるが、後で示すように、これは成分に分解しているためにそうなるだけで、速度全体Vとしては加速することは決してない。

---

微小時間後の速度

 
 
式(1-5)より、微小時間δt後の速度bは、
\[ {\Large \fbox{ $ \displaystyle{ \begin{align} b=&a-{(f\cdot\sin{\theta}-g)}\cdot\delta{t} \\ \end{align} } $ } } \]
となる。