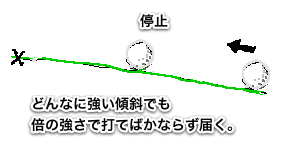
平面の2倍の強さで打てば必ず届く

いきなりどう曲がるかを求める前に、最も単純なケースを具体的に考えておこう。

つまり、真っ直ぐの上りと下りです。


意外に分かっているようで分かっていないのは、上りのときの打つ強さです。


それでは問題です。

問題1
　真っ直ぐの上りで、どんなに傾斜が強くても、
　平面の時の何倍の強さでボールを打てば、
　少なくとも平面のときと同じ距離だけ進むでしょうか?
　ただし、必ず止まるものとします。

どんなに傾斜が急になっても、ものすごく強く打てば止めたい位置をはるかに越えてしまう。打つ強さの限度がどこにあるのか、意外ですが誰もよくわかっていない。ゴルフの本にも書いてないし、誰も教えてくれない。


上りで進む距離Luは、大きさだけを考えれば、式(1-4)から、


\[ {\Large \fbox{ $ \displaystyle{ \begin{align} \left|{L_{u}}\right|= L\cdot\frac{1}{f+g} \\ \end{align} } $ } } \]


と表わせる。(L,f,g > 0)


g= fのときには、摩擦と傾斜の強さが釣り合って、いつまでも転がり続ける。だから、必ず止まるということは、限度はg= fということです。
つまり、f= 1なので、|L_u|= L/2となる。
平面のときのちょうど半分の距離しか進まない。


言い換えれば、2倍の強さで打てばどんな傾斜でも必ず届くということです。

言われてみれば、ありそうな答えだと思える。
しかし、ゴルファーはそんなことも知らずに(教えられずに)プレーをしている。
限度を知れば、少しは不安が解消できるはずです。


傾斜の強さg=1のときの傾斜角θで示すように、約6度の傾斜角(典型的なグリーンスピード7.5ftの場合)がg= f =1に相当する。