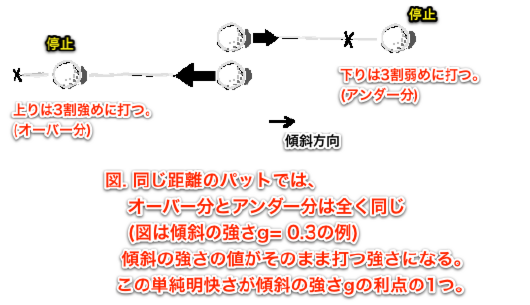
真っ直ぐの上りと下りの打つ強さ

傾斜の強さgの値だけ、例えば3割強く・3割弱く打てばいい
最も単純なケースについてもう少し考えてみよう。
ここでは、g < fの場合(必ず止まるケース)を考える。
上りも下りも同じ距離Lだけ進んで止まるものとする。
式(2-2)のLとLuを逆にして、平面なら距離Luで止まるような強さで打った場合に、実際には距離Lだけ上って止まったと考えればいい。下りの場合(距離Ldとする)も同様です。よって、
\[ {\Large \fbox{ $ \displaystyle{ \begin{align} L=& \color{green}{-}L_{u}\cdot\frac{1}{f+g} \\ L=& \hspace{6pt}L_{d}\cdot\frac{1}{f-g}\\ \end{align} } $ } } \]
である。Luにマイナス符号がついているのは、-Y方向(上り方向)の意味です。
これを変形すると、
\[ {\Large \fbox{ $ \displaystyle{ \begin{align} L_{u}=& -(f\cdot L+\color{red}{g\cdot L)} \\ L_{d}=& \hspace{10pt}f\cdot L-\color{red}{g\cdot L} …{\normalsize(2-5)}\\ \end{align} } $ } } \]
となる。
これは上りの場合はg・Lだけオーバーするつもりで打ち、
下りの場合はg・Lだけ短めに打てばいい、ということを表している。
通常はf= 1と考えればいいので、f・Lは転がしたい距離Lと同じです。
たとえば、g= 0.3の場合、上りでは、止めようとする位置の1.3倍の地点を狙って打てばいいし(1.3倍の強さで打つ)、下りの場合は、0.7倍の距離を転がすつもりで打てばいい。
「1.3倍の強さで打つ」というのは、平面なら1.3倍の距離だけ転がるという意味です。全ては平面を基準に考えるからです。
gの値そのもの なので、非常に分かりやすい。
真っ直ぐの転がりというのは、実に単純です。
信じ難いことですが、 ゴルファーは、こんな単純な関係すら知らずに プレーしてきた。
傾斜の強さを力gとして表すことは、このような利点を生む 。
しかし、 曲がり方はこんなに単純ではない 。