パターでボールをヒットした(撃力を加えた)ときに、
回転(正回転あるいはバックスピン)を加えた場合を考えてみよう。

回転を並進速度に換算する

 
 
パットした瞬間に回転を加えることをどのように表わせばいいだろう?
 

 
並進速度Vのときの回転を並進速度に換算して、

• γ・V

と表わすことにする。
γが負の値のとき、バックスピンがかかっていることを表わす。
 
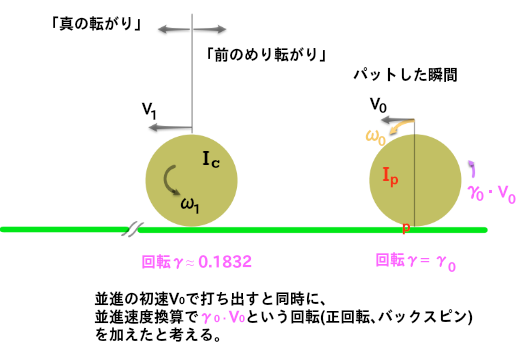
例えば、パットした瞬間に、
並進の初速V₀と同時に、回転(正回転､バックスピン)を加えた場合、
その回転は、

• γ₀・V₀

と表わされる。
 
回転を与えずにパットした瞬間はγ=0で、
「真の転がり」に相当する回転は､γ≈0.1832です。
 
これが1つの画期的なアイデアです。
ありそうでなかった、「コロンブスの卵」と言っていいでしょう。
このようにすると、考え方を単純化できるし、
結果として式もシンプルになる。
 
そして、正回転、バックスピンの全容を明らかにできたのも、
このアイデアがあったからこそです。
 
以下のような利点がある。

並進速度と回転を単純に加減算できる (利点)

回転を並進速度に換算している利点は、単純に加減算できることです。
それは、エネルギーや運動量を考える時に特に重要です。


一般的には、ボールの全エネルギーは、
並進のエネルギーと回転のエネルギーを加えたものです。
つまり、速度や角速度を2乗した後で加える。


それに対して、回転を並進速度に換算した場合は、以下のように
加算してから2乗すればいい。


同様に、運動量が保存される場合にも、加減算ができる。
ボールの質量は同じなので､運動量の加算は､速度の加算と同じです。


\[ {\Large \fbox{ $ \displaystyle{ \begin{align} 全エネルギー&=(V_{0}+\gamma_{0}V_{0})^{2}\\ 全運動量&= V_{0}+\gamma_{0}V_{0}\\\\ ただし、　&\\ \gamma_{0}&\geq0:正回転\\ \gamma_{0}&=0:回転を加えない\\ \gamma_{0}&\leq0:バックスピン\\ \gamma_{0}&:加えた回転を並進速度換算する係数\\ \end{align} } $ } } \]


以下で「真の転がり」に相当するγ値を計算するときにも、この理屈が活かされている。


分かりやすい例で言えば、
時速10km/hに10km/hを加えれば、20km/hになるのと同じ理屈です。
決して10km/hを2乗してから加えたものが全エネルギーではなく、加えた後の20km/hを2乗したものが全エネルギーです。

「真の転がり」に相当する回転 (γ_t≈+0.1832)

「真の転がり」に相当するγ値は、γ=+1ではない。
γ値は回転を並進速度に換算した値だからです。


全エネルギーがそのまま真の転がりになったと仮定すると、以下のような式で表わされる。


ここで注意が必要なのは、回転が並進速度に換算されていることです。
並進速度同士は加算できるので、加算してから2乗を取ったものが、全エネルギーです。


\[ {\Large \fbox{ $ \displaystyle{ \begin{align} &真の転がりに相当する回転\gamma_{t}: \\ &\underbrace{({V_{0}+\gamma_{t}V_{0}})^{2}}_{全エネルギー}\times\underbrace{\frac{5}{7}}_{並進のエネルギーの比率}=\underbrace{V_{0}^{\hspace{3pt}2}}_{並進のエネルギー}\\ \therefore& \gamma_{t}=\left\{{\sqrt[]{\frac{7}{5}}}\right\}-1\approx0.1832\\ &V_{0}:並進の初速\\ &\gamma_{t}:真の転がりに相当する回転を並進速度換算する係数\\ \end{align} } $ } } \]


ただし、γ_t≈+0.1832という正回転を与えることは、
最初から「真の転がり」になると言うことではない。


ここは理解が難しいところです。


簡単に言えば、慣性の法則に従っているので、
止まっていたものが瞬間的に「真の転がり」の状態になることはできないからです。

「真の転がり」に相当するバックスピン (−γ_t≈ −0.1832)

同様の理屈で、
γ= −γ_t= −0.1832のときに並進の速度を打ち消して、前進も後退もしないと言うことではない。

ロングパットほど加える回転は大きくなる(γ値は常に一定)

回転係数γが常に一定と仮定したとしても、
初速が大きくなればなるほど加える回転も大きくなることを意味する｡
回転を初速の何倍かで表わしたものがγ値だからです。


ボールの初速に比例して加える回転も大きくなるのが自然なので､矛盾はない｡


打つ強さを大きくしつつ､回転を弱くしようとするのは、かえって難しい。


回転を加えようとする心理は､
最初から「真の転がり」にするつもりでパットしているはずです｡
そういう心理がγ値を一定にさせるとも言える｡


短いパットは､それ相当の弱い回転を加えようとするでしょう。
ロングパットになれば､それなりに強い回転を加えようとするはずです｡
γ値が一定と考えるほうが､より現実的と言うことです｡


だから､打つ強さ(初速)を変えても､γ値は常に一定と仮定する｡


現実的には､生身の人間がパットするのですから､
打つ強さで多少の変化はあるのは当然ですが､
先ずは一定と考えてみることが科学的なアプローチには必要だからです｡


もしも教科書的に､回転を絶対値として考えると､打つ強さを変えた時に､加える回転をどのように変化させるかが問題になる｡


この点でも､回転を並進速度換算することのメリットがある。
シンプルなので､理解しやすいし、現実的でもある。