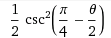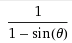LinkIcon参考文献[11]の解釈の誤り





「詳解 力学演習　後藤慶一、山本邦夫など共編(共立出版 1971)」

解の不完全さ





参考文献[11]のP.103の設問[14]の解は以下のように示されている。
\[ {\Large \fbox{ $ \displaystyle{ \begin{align} V &= V_{0}\frac{\tan^{\lambda}{\phi}}{\cos{\theta}}\\ &= \frac{V_{0}}{2}\sin^{\lambda-1}{\phi}\cdot\cos^{-\lambda-1}{\phi}\\ &= \frac{V_{0}}{2}\tan^{\lambda-1}{\phi}\cdot\cos^{-2}{\phi} \space\space\space…{\normalsize(f)}\\ &ただし、\phi=\frac{\theta}{2}+\frac{\pi}{4}\\ &　　　　\lambda=\frac{\mu}{\tan{\alpha}}\\ &　　　　\alpha: 傾斜角\\ &　　　　\mu: 粗い斜面と質点との摩擦係数\\ &　　　　\theta=0\sim\frac{\color{red}{-}\pi}{2}\\ \end{align} } $ } } \]

「λ=1のときに、θ→ −π/2でV→V0/2となり、θ=−π/2に漸近する」
と書かれているが、これは誤りです。


確かに､式(f)は、λ=1かつθ=−π/2のときに、sinの項やtanの項がゼロのゼロ乗となって計算不能です。
漸近というのは、無限のかなたで限りなく近づくということ、すなわち極限値です。


この式だけを見ると､確かに､θ=−π/2のときに確定した値がないように見える。
ところが､実は､ここは特異点なので､最初からλ=1として解き直す必要がある。

λ=1とは?





λ=μ/tanα=1とは、いわゆる摩擦角の状態で､傾斜方向の力がつり合っていることを示している。
この設問[14]は質点のケースですが､転がりの場合の傾斜の強さg=1に相当する。
正確にλ=1である確率は100%であるのは、明らかです。

λ=1として解き直す





λ=1として解き直すと､
\[ {\Large \fbox{ $ \displaystyle{ \begin{align} V &= \frac{V_{0}}{2}\cdot\cos^{-2}{\phi}\\ &=\frac{V_{0}}{1-\sin{\theta}}\space\space\space…{\normalsize(f-2)} \end{align} } $ } } \]

完全な解(一般解と特異解)

つまり、完全な解は、場合分けして､


\[ {\Large \fbox{ $ \displaystyle{ \begin{align} \lambda\ne1&の場合(一般解): \\ V &= V_{0}\frac{\tan^{\lambda}{\phi}}{\cos{\theta}}\\ &= \frac{V_{0}}{2}\sin^{\lambda-1}{\phi}\cdot\cos^{-\lambda-1}{\phi}\\ &= \frac{V_{0}}{2}\tan^{\lambda-1}{\phi}\cdot\cos^{-2}{\phi} \space\space\space…{\normalsize(f)}\\ \lambda=1&の場合(特異解): \\ V &= \frac{V_{0}}{2}\cdot\cos^{-2}{\phi}\\ &=\frac{V_{0}}{1-\sin{\theta}}\space\space\space…{\normalsize(f-2)}\\ &ただし、\phi=\frac{\theta}{2}+\frac{\pi}{4}\\ &　　　　\lambda=\frac{\mu}{\tan{\alpha}}\\ &　　　　\alpha: 傾斜角\\ &　　　　\mu: 粗い斜面と質点との摩擦係数\\ &　　　　\theta=0\sim\frac{\color{red}{-}\pi}{2}\\ \end{align} } $ } } \]


つまり、
「λ=1のときに、θ→−π/2でV→V0/2となり、θ=−π/2に漸近する」のではなく、
「λ=1のときは、θ= −π/2でV=V0/2となる」というのが正しい。

具体的な計算例(2011年)





θ= 0かつλ=1のときV0= 1として、WolframAlphaで計算してみましょう。

式(f)の最初の式(※1): V=1/cos(θ)*(tan(θ/2+pi/4))^(+1)

式(f-2)(※2): V=1/2*cos(θ/2+pi/4))^(-2)



WolframAlphaによる方程式の変形は､与える式の形によって一見異なる式に変形されますが､
グラフなどを見ると､同じと分かります。


(※1)と(※2)のグラフを見ると､全く同じことが分かります。
特に､(※1)では、π/2を直接代入すると､無限大になってしまいますが､
グラフのθ=−π/2≈ −1.57付近では､無限大になっていません。
なぜなら、(※1)の計算結果をよく見ると､WolframAlphaは特異解を正しく求めているからです。

そして、(※2)の計算結果をよく見ると、以下の式も正しく示しています。

WolframAlphaは素晴らしいですね。


いずれにしても、これはθ=−π/2のときに漸近するのではなく、
電卓でも計算が可能な確定した値としてV=V0/2になることを意味します。
本に書かれた設問[14]の解が不完全なのは、λ=1の時の式(特異点)を解き直していない(場合分けをしていない)ことです。


参考文献[11]の著者(山本邦夫氏)に以上のように2003.9.11に説明したが、理解していただけなかった。
この設問は、実際には後藤慶一氏(1917-1993)が選んだ(あるいは解いた)設問だそうです。
当人が亡くなられているので真相は闇の中ですが、
特異点を場合分けするのは解法の基本なので､それを怠ったことは紛れもない事実です。